Кластерный анализ
Кластерный анализ - это совокупность методов классификации многомерных наблюдений или объектов, основанных на определении понятия расстояния между объектами с последующим выделением из них групп наблюдений (кластеров, таксонов).Назначение. С помощью онлайн-калькулятора можно проводить классификацию объектов алгоритмами «ближайшего соседа» и «дальнего соседа» с построением дендрограммы.
см. также Метод К-средних
Выбор конкретного метода кластерного анализа зависит от цели классификации.
Обычной формой представления исходных данных в задачах кластерного анализа служит матрица:
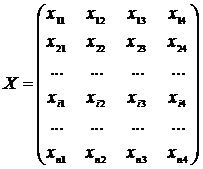
каждая строка которой, представляет результат измерений k, рассматриваемых признаков на одном из обследованных объектов.
Наиболее трудным считается определение однородности объектов, которые задаются введением расстояния между объектами хi и хj (p(xi, xj)).
Объекты будут однородными в случае p(xi, xj)£ pпор,
где pпор- заданное пороговое значение.
Выбор расстояния (р) является основным моментом исследования, от которого зависят окончательные варианты разбиения. Наиболее распространенными считаются принципы “ближайшего соседа” или “дальнего соседа”. В первом случае за расстояние между кластерами принимают расстояние между ближайшими элементами этих кластеров, а во втором - между наиболее удаленными друг от друга.
В задачах кластерного анализа часто используют Евклидово и Хемингово расстояния.
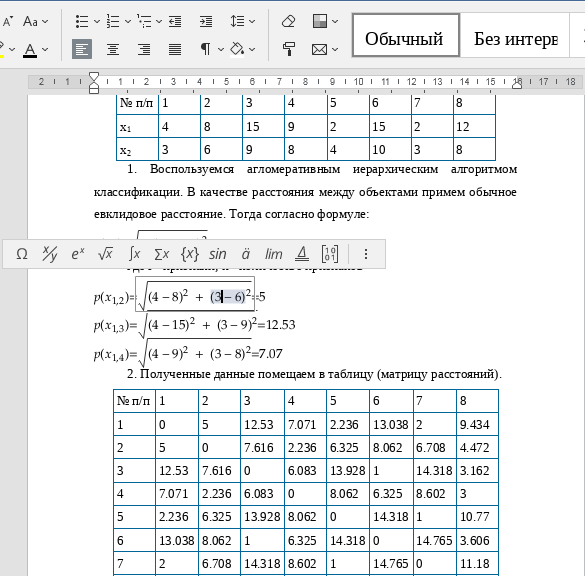
Евклидово расстояние определяется по формуле:
![]() ;
;
сравнивается близость двух объектов по большому числу признаков.
Хемингово расстояние:
![]() ;
;
используется как мера различия объектов, задаваемых атрибутивными признаками.
Пример. Провести классификацию шести объектов, каждый из которых характеризуется двумя признаками (табл.9). В качестве расстояния между объектами принять , расстояние между кластерами исчислить по принципам: 1) “ближайшего соседа” и 2) “дальнего соседа”.
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 |
| x1 | 2 | 4 | 5 | 12 | 14 | 15 |
| x2 | 8 | 10 | 7 | 6 | 6 | 4 |
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0 | 2.83 | 3.16 | 10.2 | 12.17 | 13.6 |
| 2 | 2.83 | 0 | 3.16 | 8.94 | 10.77 | 12.53 |
| 3 | 3.16 | 3.16 | 0 | 7.07 | 9.06 | 10.44 |
| 4 | 10.2 | 8.94 | 7.07 | 0 | 2 | 3.61 |
| 5 | 12.17 | 10.77 | 9.06 | 2 | 0 | 2.24 |
| 6 | 13.6 | 12.53 | 10.44 | 3.61 | 2.24 | 0 |
Из матрицы расстояний следует, что объекты 4 и 5 наиболее близки P4;5 = 2 и поэтому объединяются в один кластер.
| № п/п | 1 | 2 | 3 | [4] | [5] | 6 |
| 1 | 0 | 2.83 | 3.16 | 10.2 | 12.17 | 13.6 |
| 2 | 2.83 | 0 | 3.16 | 8.94 | 10.77 | 12.53 |
| 3 | 3.16 | 3.16 | 0 | 7.07 | 9.06 | 10.44 |
| [4] | 10.2 | 8.94 | 7.07 | 0 | 2 | 3.61 |
| [5] | 12.17 | 10.77 | 9.06 | 2 | 0 | 2.24 |
| 6 | 13.6 | 12.53 | 10.44 | 3.61 | 2.24 | 0 |
В результате имеем 5 кластера: S(1), S(2), S(3), S(4,5), S(6)
Из матрицы расстояний следует, что объекты 4,5 и 6 наиболее близки P4,5;6 = 2.24 и поэтому объединяются в один кластер.
| № п/п | 1 | 2 | 3 | [4,5] | [6] |
| 1 | 0 | 2.83 | 3.16 | 10.2 | 13.6 |
| 2 | 2.83 | 0 | 3.16 | 8.94 | 12.53 |
| 3 | 3.16 | 3.16 | 0 | 7.07 | 10.44 |
| [4,5] | 10.2 | 8.94 | 7.07 | 0 | 2.24 |
| [6] | 13.6 | 12.53 | 10.44 | 2.24 | 0 |
В результате имеем 4 кластера: S(1), S(2), S(3), S(4,5,6)
Из матрицы расстояний следует, что объекты 1 и 2 наиболее близки P1;2 = 2.83 и поэтому объединяются в один кластер.
| № п/п | [1] | [2] | 3 | 4,5,6 |
| [1] | 0 | 2.83 | 3.16 | 10.2 |
| [2] | 2.83 | 0 | 3.16 | 8.94 |
| 3 | 3.16 | 3.16 | 0 | 7.07 |
| 4,5,6 | 10.2 | 8.94 | 7.07 | 0 |
В результате имеем 3 кластера: S(1,2), S(3), S(4,5,6)
Из матрицы расстояний следует, что объекты 1,2 и 3 наиболее близки P1,2;3 = 3.16 и поэтому объединяются в один кластер.
| № п/п | [1,2] | [3] | 4,5,6 |
| [1,2] | 0 | 3.16 | 8.94 |
| [3] | 3.16 | 0 | 7.07 |
| 4,5,6 | 8.94 | 7.07 | 0 |
В результате имеем 2 кластера: S(1,2,3), S(4,5,6)
| № п/п | 1,2,3 | 4,5,6 |
| 1,2,3 | 0 | 7.07 |
| 4,5,6 | 7.07 | 0 |
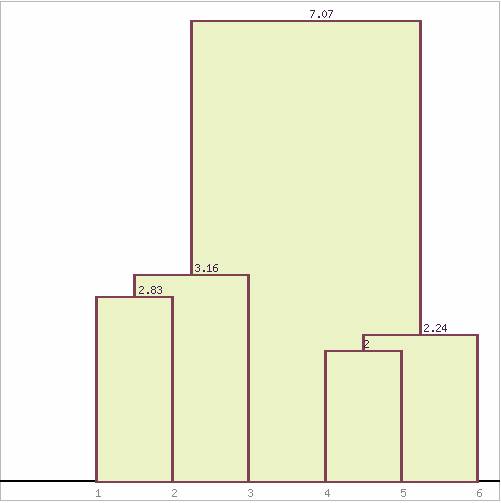
Результаты иерархической классификации объектов представлены на рис. в виде дендрограммы.
Дендрограмма