Кривая Лоренца
Назначение сервиса. С помощью онлайн-калькулятора можно рассчитать:- индекс Джини, коэффициент Лоренца;
- децильный коэффициент дифференциации доходов.
- распределение населения по уровню среднедушевых доходов – это показатель удельного веса или процента населения в тех или иных заданных интервалах среднедушевых денежных доходов.
- распределение общего объема денежных доходов по различным группам населения – показатель в процентах доли общего объема денежных доходов, которой обладает каждая из двадцати процентных (десяти процентных) групп населения. Этот показатель наглядно представил экономист Лоренц в виде кривой фактического распределения дохода (кривая Лоренца).
- децильный коэффициент дифференциации доходов – соотношение среднедушевых денежных доходов последней и первой групп населения. Он показывает, во сколько раз доходы n% наиболее обеспеченного населения превышают доходы n% наименее обеспеченного населения.
Дифференциация заработной платы предопределяет неравенство в распределении доходов.
Дифференциация доходов населения - это объективно складывающиеся различия в уровне доходов индивидов и социальных групп, обусловленные различиями в оплате труда и социальных выплат, способностях и предприимчивости, имущественном положении.
Денежные доходы населения включают в себя заработную плату, социальные трансферты, предпринимательские доходы, проценты, дивиденды и другие доходы от собственности, а также общую стоимость продукции –личного подсобного хозяйства, потребленной в семье и проданной. Доходы населения распределяются по группам населения неравномерно.
Помимо анализа распределения доходов населения, кривую Лоренца также используют при конкурентном анализе.
см. также Показатели оценки дифференциации доходов населения
Пример №1. На основе данных таблицы:
- Рассчитайте коэффициент Джини
- Постройте кривую Лоренца.
| Социальная группа населения | Численность населения, % | Денежные доходы, % |
| 1. | 20 | 6,0 |
| 2. | 20 | 11,6 |
| 3. | 20 | 17,6 |
| 4. | 20 | 26,5 |
| 5. | 20 | 38,3 |
| Итого | 100 | 100,0 |
Денежные доходы населения
| Группы по денежным доходам, % | Доля денежных доходов в группе, % |
| 20 | 6 |
| 40 | 11.6 |
| 60 | 17.6 |
| 80 | 26.5 |
| 100 | 38.3 |
Линия фактического неравенства строится на основании данных о процентах дохода приходящихся на каждые 20 % населения.
Если нижняя первая часть населения получила 6.0% всех доходов, то графически это будет точка А. Чтобы получить точку В необходимо сложить процент дохода первых 20 % населения с процентами доходов вторых 20 % населения (6.0% + 11.6%) и т.д.
| 20-ти процентные группы населения | Объем денежных доходов населения, в % к итогу | Доля денежных доходов нарастающим итогом, % | Площадь треугольника | Площадь прямоугольника | Общая площадь фигуры, Si |
| 20 | 6 | 6 | 60 | 0 | 60 |
| 40 | 11.6 | 17.6 | 116 | 120 | 236 |
| 60 | 17.6 | 35.2 | 176 | 352 | 528 |
| 80 | 26.5 | 61.7 | 265 | 704 | 969 |
| 100 | 38.3 | 100 | 383 | 1234 | 1617 |
| 3410 |
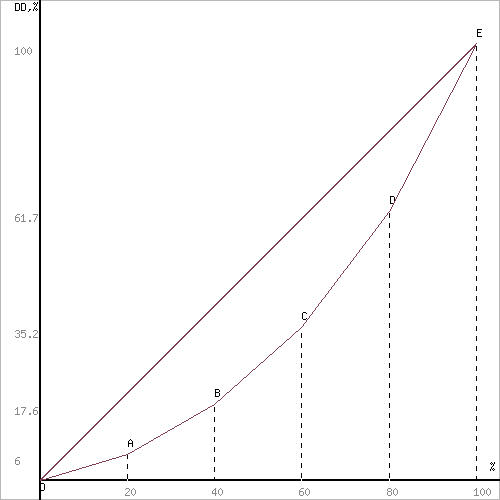
2. Индекс Джини.
Для исчисления коэффициента Джини необходимо рассчитать величины pi и qi. Здесь qi - доля денежных доходов нарастающим итогом (столбец №3 табл.1) деленная на 100.
| pi | qi | piqi+1 | pi+1qi |
| 0.2 | 0.06 | 0.0352 | - |
| 0.4 | 0.18 | 0.14 | 0.024 |
| 0.6 | 0.35 | 0.37 | 0.11 |
| 0.8 | 0.62 | 0.8 | 0.28 |
| 1 | 1 | - | 0.62 |
| ВСЕГО | 1.3462 | 1.0282 |
Пример №2. Имеются следующие данные о распределении доходов населения региона по трем группам и доле населения в каждой группе:
1 группа | 2 группа | 3 группа | |
Доходы населения по группам (руб.) | 5000-10000 | 10000-20000 | 20000-30000 |
Доля населения в группе | 0,15 | 0,60 | 0,25 |
Решение.
Необходимо найти доли среднего дохода на человека в каждой группе, в виде отношения среднего дохода группы к суммарному среднему доходу, и соответствующие накапливаемые частоты этих долей. Чем ближе значение коэффициента к единице, тем выше уровень дифференциации доходов.
1 группа | 2 группа | 3 группа | Итого | |
Доходы населения по группам (руб.) | 5000-10000 | 10000-20000 | 20000-30000 | |
Среднее значение дохода в группе, руб. | 7500 | 15000 | 25000 | 47500 |
Доля доходов в группе, % | 15,8 | 31,6 | 52,6 | 100,0 |
Доля доходов в группе, % | Доля населения в группе |
15,8 | 0,15 |
31,6 | 0,6 |
52,6 | 0,25 |
Пример №3. Дать графическое изображение вариационного ряда, приведенного в таблице (гистограмма, полигон, кумулята). Определить средние величины (меры положения) – среднюю арифметическую, моду, медиану, вычислить квартили и показатели вариации – среднее абсолютное отклонение, дисперсию, среднее квадратическое отклонение, относительный квартильный размах, коэффициент вариации. Построить кривую (ломаную) Лоренца, вычислить коэффициент концентрации дохода (индекс Джини). Пояснить статистический, физический, экономический или иной смысл вычисленных величин.
| № группа | Среднедушевые доходы населения (тыс. руб.) | Количество насосов |
| 1 | 0-30 | 10 |
| 2 | 30,1-60 | 14 |
| 3 | 60,1-90 | 19 |
| 4 | 90,1-120 | 25 |
Пример №4. Исходные данные:
| % | Доход |
| 10 | 2.3 |
| 20 | 4.5 |
| 30 | 4.7 |
| 40 | 6 |
| 50 | 7.5 |
| 60 | 10.2 |
| 70 | 14.1 |
| 80 | 16.7 |
| 90 | 18.5 |
| 100 | 15.5 |
| % | Доход | S=Si+Si-1 | Площадь треугольника | Площадь | Сумма |
| 10 | 2.3 | 2.3 | 11.5 | 0 | 11.5 |
| 20 | 4.5 | 6.8 | 22.5 | 23 | 45.5 |
| 30 | 4.7 | 11.5 | 23.5 | 68 | 91.5 |
| 40 | 6 | 17.5 | 30 | 115 | 145 |
| 50 | 7.5 | 25 | 37.5 | 175 | 212.5 |
| 60 | 10.2 | 35.2 | 51 | 250 | 301 |
| 70 | 14.1 | 49.3 | 70.5 | 352 | 422.5 |
| 80 | 16.7 | 66 | 83.5 | 493 | 576.5 |
| 90 | 18.5 | 84.5 | 92.5 | 660 | 752.5 |
| 100 | 15.5 | 100 | 77.5 | 845 | 922.5 |
| Итого | 3481 |
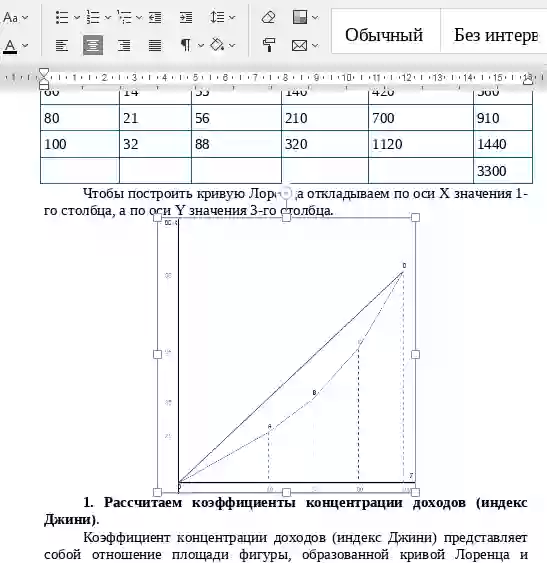
Чтобы построить кривую Лоренца откладываем по оси Х откладываем значения столбца Процент (%), а по сои Y значения столбца S.
Рассчитаем коэффициенты концентрации доходов (индекс Джини)
Уровень неравенства определяется с помощью коэффициента Джини.
Он рассчитывается как отношение площади фигуры OABCDKLMNPE к площади треугольника ОEG.
Для того чтобы определить площадь фигуры, лежащей ниже кривой Лоренца, соединяем прямыми линиями точки ОА, АВ и т.д.
Опускаем перпендикуляр на ось X и находим площади фигур, лежащих ниже точек А, B, С.
SOAA' = 1 / 2 * 10% * 2.3
Площадь SABB’A состоит из треугольника и прямоугольника SBCCB’ также состоит из треугольника и прямоугольника.
Сложив все площади фигур, получим площадь фигуры S2.
Площадь треугольника OEG находим по формуле:
1/2 *100%*100% = 5000
Отсюда индекс Джини равен:
(SOEG - S2)/ = SOEG
I = 1519 / 5000 = 0.3038
Децильный коэффициент дифференциации доходов
15.5 / 2.3 = 6.74