Мультипликативная модель временного ряда

Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.
Общий вид мультипликативной модели выглядит так:

Y = T x S x E

где T - трендовая компонента, S - сезонная компонента и E - случайная компонента.
Назначение. С помощью данного сервиса производится построение мультипликативной модели временного ряда.

Инструкция. Укажите количество данных (количество строк), нажмите Далее. На втором шаге выберите диапазон моделирования. Полученное решение сохраняется в файле MS Word и MS Excel (см. пример решения).

Скачать пример оформления

см. также Мультипликативная индексная двухфакторная модель.

Алгоритм построения мультипликативной модели

Построение мультипликативной моделей сводится к расчету значений T, S и E для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.

Выравнивание исходного ряда методом скользящей средней.
Расчет значений сезонной компоненты S.
Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (T x E).
Аналитическое выравнивание уровней (T x E) с использованием полученного уравнения тренда.
Расчет полученных по модели значений (T x E).
Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок E для анализа взаимосвязи исходного ряда и других временных рядов.

Пример. Построить аддитивную и мультипликативную модель временного ряда, характеризующую зависимость уровней ряда от времени.
Решение. Построение мультипликативной модели временного ряда.
Общий вид мультипликативной модели следующий:
Y = T x S x E
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.
Рассчитаем компоненты мультипликативной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Найдем скользящие средние (гр. 3 таблицы). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.2. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 4 табл.).

t	y_t	Скользящая средняя	Центрированная скользящая средняя	Оценка сезонной компоненты
1	898	-	-	-
2	794	1183.25	-	-
3	1441	1200.5	1191.88	1.21
4	1600	1313.5	1257	1.27
5	967	1317.75	1315.63	0.74
6	1246	1270.75	1294.25	0.96
7	1458	1251.75	1261.25	1.16
8	1412	1205.5	1228.63	1.15
9	891	1162.75	1184.13	0.75
10	1061	1218.5	1190.63	0.89
11	1287	-	-	-
12	1635	-	-	-

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 5 табл.). Эти оценки используются для расчета сезонной компоненты S. Для этого найдем средние за каждый период оценки сезонной компоненты S_j. Сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.

Показатели	1	2	3	4
1	-	-	1.21	1.27
2	0.74	0.96	1.16	1.15
3	0.75	0.89	-	-
Всего за период	1.49	1.85	2.37	2.42
Средняя оценка сезонной компоненты	0.74	0.93	1.18	1.21
Скорректированная сезонная компонента, S_i	0.73	0.91	1.16	1.19

Для данной модели имеем:
0.744 + 0.927 + 1.183 + 1.211 = 4.064
Корректирующий коэффициент: k=4/4.064 = 0.984
Рассчитываем скорректированные значения сезонной компоненты S_i и заносим полученные данные в таблицу.
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины T x E = Y/S (гр. 4 табл.), которые содержат только тенденцию и случайную компоненту.
Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a₀n + a₁∑t = ∑y
a₀∑t + a₁∑t² = ∑y•t
Для наших данных система уравнений имеет вид:
12a₀ + 78a₁ = 14659.84
78a₀ + 650a₁ = 96308.75
Из первого уравнения выражаем а₀ и подставим во второе уравнение
Получаем a₁ = 7.13, a₀ = 1175.3
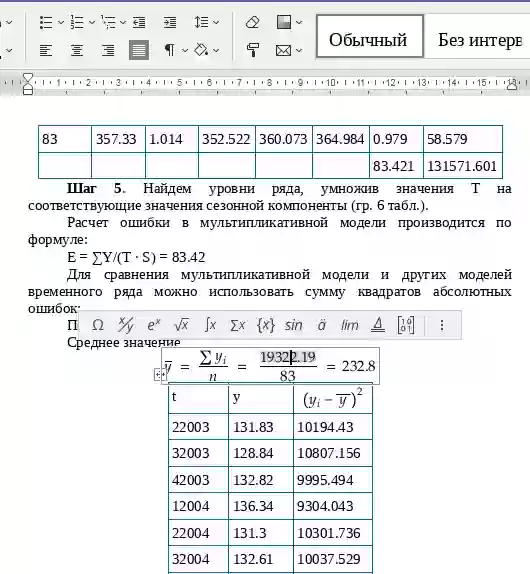
Среднее значения

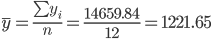
t	y	t²	y²	t•y	y(t)	(y-y_cp)²	(y-y(t))²
1	1226.81	1	1505062.02	1226.81	1182.43	26.59	1969.62
2	870.35	4	757510.32	1740.7	1189.56	123413.31	101895.13
3	1238.16	9	1533048.66	3714.49	1196.69	272.59	1719.84
4	1342.37	16	1801951.56	5369.47	1203.82	14572.09	19194.4
5	1321.07	25	1745238.05	6605.37	1210.96	9884.65	12126.19
6	1365.81	36	1865450.09	8194.89	1218.09	20782.63	21823.45
7	1252.77	49	1569433.89	8769.39	1225.22	968.3	759.1
8	1184.64	64	1403371.14	9477.12	1232.35	1369.99	2276.31
9	1217.25	81	1481689.26	10955.22	1239.48	19.42	494.41
10	1163.03	100	1352627.82	11630.25	1246.61	3437.21	6987
11	1105.84	121	1222883.47	12164.25	1253.75	13412.51	21875.75
12	1371.73	144	1881649.21	16460.79	1260.88	22523.77	12288.93
78	14659.84	650	18119915.49	96308.75	14659.84	210683.05	203410.13

Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
T = 1175.298 + 7.132t
Подставляя в это уравнение значения t = 1,...,12, найдем уровни T для каждого момента времени (гр. 5 табл.).

t	y_t	S_i	y_t/S_i	T	TxS_i	E = y_t / (T x S_i)	(y_t - T*S)²
1	898	0.73	1226.81	1182.43	865.51	1.04	1055.31
2	794	0.91	870.35	1189.56	1085.21	0.73	84801.95
3	1441	1.16	1238.16	1196.69	1392.74	1.03	2329.49
4	1600	1.19	1342.37	1203.82	1434.87	1.12	27269.14
5	967	0.73	1321.07	1210.96	886.4	1.09	6497.14
6	1246	0.91	1365.81	1218.09	1111.23	1.12	18162.51
7	1458	1.16	1252.77	1225.22	1425.93	1.02	1028.18
8	1412	1.19	1184.64	1232.35	1468.87	0.96	3233.92
9	891	0.73	1217.25	1239.48	907.28	0.98	264.9
10	1061	0.91	1163.03	1246.61	1137.26	0.93	5814.91
11	1287	1.16	1105.84	1253.75	1459.13	0.88	29630.23
12	1635	1.19	1371.73	1260.88	1502.87	1.09	17458.67

Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл.).
Расчет ошибки в мультипликативной модели производится по формуле:
E = Y/(T * S) = 12
Для сравнения мультипликативной модели и других моделей временного ряда можно использовать сумму квадратов абсолютных ошибок:
Среднее значения

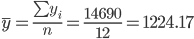
t	y	(y-y_cp)²
1	898	106384.69
2	794	185043.36
3	1441	47016.69
4	1600	141250.69
5	967	66134.69
6	1246	476.69
7	1458	54678.03
8	1412	35281.36
9	891	111000.03
10	1061	26623.36
11	1287	3948.03
12	1635	168784.03
78	14690	946621.67

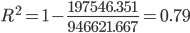
Следовательно, можно сказать, что мультипликативная модель объясняет 79% общей вариации уровней временного ряда.
Проверка адекватности модели данным наблюдения.

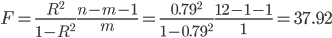
где m - количество факторов в уравнении тренда (m=1).
Fkp = 4.96
Поскольку F> Fkp, то уравнение статистически значимо
Шаг 6. Прогнозирование по мультипликативной модели. Прогнозное значение F_t уровня временного ряда в мультипликативной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда:T = 1175.298 + 7.132t
Получим
T₁₃ = 1175.298 + 7.132*13 = 1268.008
Значение сезонного компонента за соответствующий период равно: S₁ = 0.732
Таким образом, F₁₃ = T₁₃ + S₁ = 1268.008 + 0.732 = 1268.74
T₁₄ = 1175.298 + 7.132*14 = 1275.14
Значение сезонного компонента за соответствующий период равно: S₂ = 0.912
Таким образом, F₁₄ = T₁₄ + S₂ = 1275.14 + 0.912 = 1276.052
T₁₅ = 1175.298 + 7.132*15 = 1282.271
Значение сезонного компонента за соответствующий период равно: S₃ = 1.164
Таким образом, F₁₅ = T₁₅ + S₃ = 1282.271 + 1.164 = 1283.435
T₁₆ = 1175.298 + 7.132*16 = 1289.403
Значение сезонного компонента за соответствующий период равно: S₄ = 1.192
Таким образом, F₁₆ = T₁₆ + S₄ = 1289.403 + 1.192 = 1290.595

Мультипликативная модель временного ряда

Алгоритм построения мультипликативной модели

Правила ввода данных

Поиск

Процесс

Сообщение

Подключить услуги