Модель взаимозачета долгов предприятий
Онлайн-калькулятор предназначен для оптимизации взаимных долгов предприятий.Поясним суть проблемы на примере для системы из трех предприятий, каждое из которых имеет свободные средства, равные условно одной финансовой единице, и основные фонды, равные 10 единицам. Пусть первое предприятие должно второму 100 единиц, второе должно третьему 100 единиц, и, наконец, третье первому также 100 единиц. Суммарный абсолютный долг предприятий равен 600 единицам и огромен в сравнении с их фондами 30 единиц), не говоря уже о свободных средствах C единицы). В то же время финансовое положение этой системы фактически благополучное, так как суммарный «долг» каждого предприятия в отдельности (т. е. сумма средств, которые предприятие должно другим, и другие должны ему) равен нулю. Очевидная процедура взаимозачета состоит в одномоментном аннулировании (погашении) всех долгов: объявляется, что
никто никому не должен, и партнеры продолжают свою работу, будучи свободными от долгового бремени. Централизованный кредит при этом, естественно, вообще не требуется.
Подобную операцию, произведенную «вручную», нельзя, конечно, реализовать для большого числа предприятий с огромным количеством финансовых обязательств. Требуются более глубокие подходы, для рассмотрения которых необходимо, прежде всего, формализовать задачу.
Итак, пусть экономическая система состоит из N предприятий, могущих иметь взаимные долги. Обозначим долги n-го предприятия m-му через xnm, где n≥1, m≤N (xnm<0, если первое предприятие должно второму, и xnm>0 в обратном случае). Ясно, что xnm=-xmn, т. е. совокупность долгов описывается кососимметричной матрицей размера NxN с нулевой диагональю (xnn=0, поскольку предприятие самому себе должно быть не может).
Сумма всех взаимных долгов вычисляется через индивидуальные
долги по простой формуле
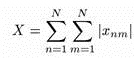 , (7)
, (7)
Величина (7) служит одной из интегральных количественных характеристик финансового положения системы: если она сопоставима с суммой всех свободных средств предприятий X0, т. е.
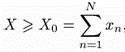 , (8)
, (8)
то описываемая неравенством (8) ситуация и означает кризис неплатежей (здесь xn≥0 — индивидуальные свободные средства предприятий).
Еще одна важная характеристика — баланс кредитов и долгов (сальдо) каждого предприятия
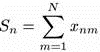 , (9)
, (9)
причем, как очевидно из (9), возможны варианты Sn>0, Sn<0, Sn=0. При Sn>0 предприятие является в некотором смысле кредитором предприятии-должников, т. е. тех, у кого Sn<0 (при Sn=0 предприятие в отношении долгов «нейтрально»). При |Sn|<xn индивидуальное финансовое состояние предприятия по существу нормальное, поскольку его реальные суммарные долги (или кредиты, «данные» им другим) меньше его свободных средств.
Аналогично, суммарное абсолютное сальдо системы
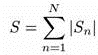 , (10)
, (10)
служит макропоказателем ее возможного финансового «здоровья». Если S<X0, то свободных средств в системе больше, чем действительных долгов, и потенциально она может успешно функционировать (подобно системе трех предприятий из приведенного выше примера).
Между величинами X и S всегда существует определенное соотношение. Для любой произвольной матрицы долгов выполняется неравенство
X≥S, (11)
т.е. суммарный долг никак не может быть меньше суммарного сальдо.
Задача погашения взаимных долгов состоит в том, чтобы, зная матрицу xnm, найти матрицу x'nm «новых» долгов, для которой выполнялось бы X'<X. Очевидно, что идеальным ее решением было бы X'=S, т. е. когда неравенство (11) становится равенством. Заметим, что тогда для благополучной по существу системы с S≤X0 достигалось бы соотношение X'=S≤X0, и после взаимозачета она могла бы нормально работать (хотя уменьшение величины X в любом случае полезно).
При построении математической модели процедуры взаимозачета долгов последовательно используется ряд действий, аналогичных проводимым при исследовании естественнонаучных объектов. Первое из них — отказ на определенном этапе от детального рассмотрения множества индивидуальных долгов и соответствующих связей между предприятиями.
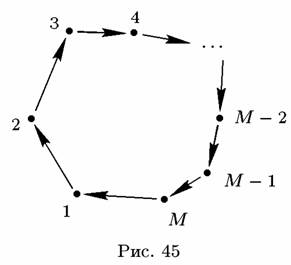
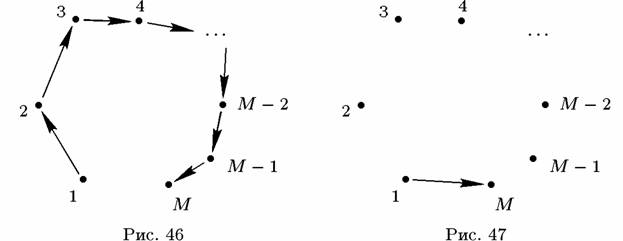
Пусть теперь М-е предприятие не должно первому (рис. 46). Тогда цепочка разомкнута, и этот метод неприменим. В то же время простое решение заключается в том, что долги предприятий со второго по (М—1)-е аннулируются, а долг первого переадресовывается М-му (рис. 47). Экономический смысл переадресации соответствует вексельному обращению, когда долговое обязательство меняет своих хозяев, и в результате у должника (первое предприятие) появляется новый кредитор (М-е предприятие).
В отличие от ситуации с долгами в цепочках полная система долгов по всем цепочкам замкнута, так как рассматриваются взаимные долги. В самом деле, из свойства xnm=-xmn следует, что
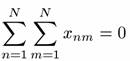
для любой совокупности неплатежей. Учитывая, что
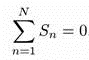 , (12)
, (12)
или
т. е. сумма положительных сальдо предприятий равна по абсолютной величине сумме отрицательных сальдо. Рассматриваемая на макроуровне система взаимных долгов обладает свойством «симметричной консервативности» (13), а «закон сохранения» (12) — аналог обычных законов сохранения (массы, энергии и т. д.) применительно к изучаемой ситуации.
Равенство (13) проясняет построение математической модели идеального взаимозачета, который производится при следующих естественных условиях:
- все долги xnm известны и признаются предприятиями;
- при проведении взаимозачета сальдо предприятий Sn остаются неизменными: S'n=S0, т. е. индивидуальное финансовое положение каждого из них в этом смысле не изменяется;
- часть долгов xnm списывается, а часть переадресовывается, т. е. у предприятий могут появиться новые должники и кредиторы и исчезнуть часть старых.
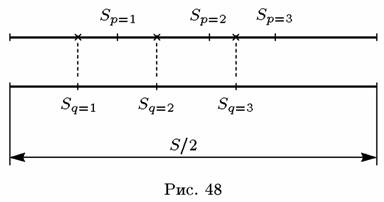
Согласно алгоритму (14) долг любого предприятия (равный Sn, если Sn<0) расписывается по предприятиям-кредиторам в долях, пропорциональных величинам их сальдо (равным Sm, если Sm>0). Предприятиям с большим положительным сальдо причитается от каждого из должников большая часть его долгов, причем в сумме они дают величину Sm. Для предприятий с нулевым сальдо взаимозачет сводится к погашению всех их долгов и всех долгов им. Заметим, что в решении (14) для новых долгов имеем x'nm = 0 при Sn<0, Sm<0 либо при Sn>0, Sm> (после взаимозачета должники не должны должникам, а кредиторы — кредиторам). Это означает, что число получившихся финансовых связей между предприятиями значительно меньше максимально возможного, когда каждое предприятие является должником или кредитором любого другого, и матрица долгов не имеет нулевых элементов (кроме, разумеется, диагональных). Количество связей может быть значительно уменьшено, если провести предварительное упорядочивание предпрятий по абсолютным значениям их сальдо и установить непосредственные связи между должниками и кредиторами одного масштаба (крупных с крупными, мелких с мелкими и т. д.). Эта процедура допускает простую геометрическую интепретацию. На рис. 48 на верхней прямой линии описано распределение сальдо кредиторов (в убывающем порядке). Длина отрезков этой прямой равна величине сальдо каждого предприятия Sp>0, 1<p<N, а её общая длина, очевидно, равна S/2. На нижней прямой описано распределение сальдо должников Sq<0, 1<q<N, p+q≤N (сальдо взяты с обратным знаком) также в убывающем порядке. Ее длина согласно (13) также равна S/2. Штриховые линии, проведенные из узлов нижней прямой, делят «прямую кредиторов» на q отрезков, равных величине долга каждого предприятия. Этот долг либо достается одному кредитору, либо делится между несколькими в соответствии с расположением узлов верхней прямой относительного данного отрезка.
Источник. Математическое и компьютерное моделирование в учебных исследованиях.
Пример. Взаимные долги 6 предприятий представлены в таблице (в млн. руб.):
| Предприятия | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0 | 20 | 50 | -60 | -125 | 100 |
| 2 | -20 | 0 | 130 | 70 | -100 | -20 |
| 3 | -50 | -130 | 0 | -60 | 160 | 50 |
| 4 | 60 | -70 | 60 | 0 | -100 | 150 |
| 5 | 125 | 100 | -160 | 100 | 0 | -200 |
| 6 | -100 | 20 | -50 | -150 | 200 | 0 |
Решение. Первоначальные долги предприятий:
Сумма всех долгов: 2790
Сальдо каждого предприятия:
S1 = ∑s1 = -15
S2 = ∑s2 = 60
S3 = ∑s3 = -30
S4 = ∑s4 = 100
S5 = ∑s5 = -35
S6 = ∑s6 = -80
Суммарное абсолютное сальдо системы: ∑∑abs(sij) = 320
Баланс системы: 0
Полученные долги предприятий:
s21 = (60 • abs(-15)-(-15) • abs(60))/320 = 5.625
s31 = (-30 • abs(-15)-(-15) • abs(-30))/320 = 0
s32 = (-30 • abs(60)-60 • abs(-30))/320 = -11.25
s41 = (100 • abs(-15)-(-15) • abs(100))/320 = 9.375
s42 = (100 • abs(60)-60 • abs(100))/320 = 0
s43 = (100 • abs(-30)-(-30) • abs(100))/320 = 18.75
s51 = (-35 • abs(-15)-(-15) • abs(-35))/320 = 0
s52 = (-35 • abs(60)-60 • abs(-35))/320 = -13.125
s53 = (-35 • abs(-30)-(-30) • abs(-35))/320 = 0
s54 = (-35 • abs(100)-100 • abs(-35))/320 = -21.875
s61 = (-80 • abs(-15)-(-15) • abs(-80))/320 = 0
s62 = (-80 • abs(60)-60 • abs(-80))/320 = -30
s63 = (-80 • abs(-30)-(-30) • abs(-80))/320 = 0
s64 = (-80 • abs(100)-100 • abs(-80))/320 = -50
s65 = (-80 • abs(-35)-(-35) • abs(-80))/320 = 0
| 0 | -5.625 | 0 | -9.375 | 0 | 0 |
| 5.625 | 0 | 11.25 | 0 | 13.125 | 30 |
| 0 | -11.25 | 0 | -18.75 | 0 | 0 |
| 9.375 | 0 | 18.75 | 0 | 21.875 | 50 |
| 0 | -13.125 | 0 | -21.875 | 0 | 0 |
| 0 | -30 | 0 | -50 | 0 | 0 |
Сальдо каждого предприятия:
S1 = ∑s1 = -15
S2 = ∑s2 = 60
S3 = ∑s3 = -30
S4 = ∑s4 = 100
S5 = ∑s5 = -35
S6 = ∑s6 = -80
Суммарное абсолютное сальдо системы: 320
Баланс системы: 0