Метод анализа иерархий
Метод анализа иерархий (Analytic Hierarchy Process - AHP), или подход аналитической иерархии предполагает декомпозицию проблемы на простые составляющие части и обработку суждений лица, принимающего решения (ЛПР). В результате определяется относительная значимость исследуемых альтернатив для всех критериев, находящихся в иерархии. Относительная значимость выражается численно в виде векторов приоритетов. Полученные таким образом значения векторов являются оценками в шкале отношений и соответствуют так называемым жестким оценкам.Назначение. С помощью онлайн-калькулятора производятся вычисление коэффициентов важности для элементов каждого уровня - индексы однородности и отношения однородности.
Постановка задачи, решаемой с помощью метода анализа иерархий, заключается обычно в следующем.
Дано: общая цель решения задачи; критерии оценки альтернатив; альтернативы. Требуется: выбрать наилучшую альтернативу.
Подход AHP состоит из совокупности этапов:
1. Структуризация задачи виде иерархической структуры с несколькими уровнями: цели – критерии – альтернативы.
2. Попарное сравнение элементов каждого уровня лицом, принимающим решения. Результаты сравнения имеют числовой характер.
3. Вычисление коэффициентов важности для элементов каждого уровня. Проверка согласованности суждений ЛПР.
Подсчет количественной оценки качества альтернатив. Выбор лучшей альтернативы.
Для установления относительной важности элементов иерархии используется шкала отношений. Данная шкала позволяет ЛПР ставить в соответствие степеням предпочтения одного сравниваемого объекта перед другим некоторые числа (таблица 2).
Таблица 2. Шкала отношений
| Степень значимости | Определение | Объяснение |
| 1 | Одинаковая значимость | Два действия вносят одинаковый вклад в достижение цели |
| 3 | Некоторое преобладание значимости одного действия над другим | Существуют соображения в пользу предпочтения одного из действий, однако эти соображения недостаточно убедительны |
| 5 | Существенная или сильная значимость | Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий |
| 7 | Очевидная или очень сильная значимость | Убедительное свидетельство в пользу одного действия перед другим |
| 9 | Абсолютная значимость | Свидетельства в пользу предпочтения одного действия перед другим в высшей степени убедительны |
| 2, 4, 6, 8 | Промежуточные значения между двумя соседними суждениями | Ситуация, когда необходимо компромиссное решение |
| Обратные величины приведенных выше величин | Если действию i при сравнением с действием j приписывается одно из определенных выше чисел, то действию j при сравнении с действием i приписывается обратное значение | Если согласованность была постулирована при получении N числовых значений для образования матрицы |
Для этого в иерархии выделяют элементы двух типов: элементы – родители и элементы – потомки. Элементы – потомки воздействуют на соответствующие элементы вышестоящего уровня иерархии, являющиеся по отношению к первым элементами – родителями. Матрицы парных сравнений строятся для всех элементов – потомков, относящихся к определенному родителю. Парные сравнения производятся в терминах доминирования одного элемента над другим в соответствии со шкалой отношений.
Если элемент Е1 доминирует над элементом Е2, то клетка матрицы, соответствующая строке Е1 и столбцу Е2, заполняется целым числом, а клетка, соответствующая строке Е2 и столбцу Е1, заполняется обратным к нему числом.
При проведении парных сравнений следует отвечать на вопросы: какой из двух сравниваемых элементов важнее или имеет большее воздействие, какой более вероятен и какой предпочтительнее.
При сравнении критериев обычно спрашивают, какой из критериев более важен; при сравнении альтернатив по отношению к критерию – какая из альтернатив более предпочтительна или более вероятна.
Теорема 1. В положительной обратносимметрической квадратной матрице λmax≥n.
Теорема 2. Положительная обратносимметрическая квадратная матрица А согласованна тогда и только тогда, когда λmax=n.
Таким образом, для оценки однородности суждений эксперта можно использовать отклонение величины максимального собственного значения λmax от порядка матрицы n.
Согласованность суждения оценивается индексом однородности (индексом согласованности) или отношением однородности (отношением согласованности) в соответствии со следующими формулами:
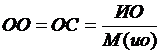
M(ио) - среднее значение индекса однородности случайным образом составленной матрицы парных сравнений, которое основано на экспериментальных данных. Значение есть табличная величина, входным параметром выступает размерность матрицы (таблица 6).
Таблица 6. Среднее значение индекса однородности в зависимости от порядка матрицы
n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
M(ио) | 0 | 0 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 | 1,51 |
Пример. Рассмотрим матрицу парных сравнений и вычислим приближенное значение главного собственного вектора:
Просуммируем элементы каждой строки и найдем сумму всех элементов матрицы:
Нормализуя вектор Ws делением каждой координаты на величину S, получаем приближенное значение главного собственного вектора:
Приближенное значение максимального собственного значения можно найти по формуле λmax=eTAW, рассмотренной выше:
При таком вычислении главного собственного вектора и максимального собственного значения может оказаться, что согласованная в действительности матрица является несогласованной по вычислениям и наоборот.
Пример. Вычислим отношение согласованности рассматриваемой выше матрицы, взяв в качестве максимального собственного значения его точное и приближенное число.
При большей погрешности метода вычисления главного собственного вектора, отношение согласованности матрицы парных сравнений могло оказаться больше 0.01.
Желательно использовать процедуры точного нахождения собственных значений и векторов матриц. Такое пожелание превращается в требование в особо ответственных задачах.
Пример (из книги Т. Саати). Рассмотрим общее благополучие индивидуума – высший уровень иерархии. На этот уровень в основном влияют детские, юношеские и взрослые впечатления. Факторы развития и зрелости, отражающиеся в благополучии, могут включать как влияние отца и матери в отдельности, так и их совместное влияние как родителей, социоэкономический фон, отношения с братьями и сестрами, группу ровесников, школьное обучение, религиозный статус и т.д.
На перечисленные выше факторы, которые составляют второй уровень иерархии, влияют соответствующие критерии. Например, влияние отца может быть разбито на категории, включающие его темперамент, строгость, заботу и привязанность. Отношение с братьями и сестрами можно дальше характеризовать их количеством, разницей в возрасте, полом; моделирование воздействия и роли ровесников обеспечивает более яркую картину влияния друзей, обучения в школе и учителей.
В качестве альтернативной основы описания для второго уровня можно включить чувство собственного достоинства, уверенность в будущем, адаптируемость к новым людям и новым обстоятельствам и т.д., влияющих или находящихся под влиянием расположенных выше элементов.
Более полная основа психологической предыстории может включать несколько сотен элементов на каждом уровне, выбранных экспертами и расположенных таким образом, чтобы получить максимальное понимание рассматриваемого индивидуума.
Рассмотрим ограниченный случай, где испытуемый чувствует, что уверенность в его силы подорвана и его социальная приспособляемость ослаблена запретами в детстве. Ему задают вопросы только о детских впечатлениях и просят попарно установить связь между следующими элементами на каждом уровне.
Построим иерархию, в которой: ОБ – общее благополучие; Д – чувство собственного достоинства; У – чувство уверенности в будущем; А – способность адаптироваться к другим; П – явная привязанность, проявленная по отношению к субъекту; Э – идеи строгости, этики; Н – действительное наказание ребенка; Л – подчеркивание личной приспособляемости к другим; М – влияние матери; О – влияние отца; Р – влияние обоих родителей.
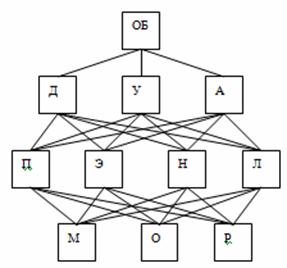
Рисунок 1 - Иерархическая схема общего благополучия индивидуума
WОБ=(0.701; 0.193; 0.106), λmax=3.26; ИС=0.07; OC=0.12
WД=(0.604; 0.213; 0.064; 0.119), λmax=4.35; ИС=0.12; OC=0.13
WУ=(0.604; 0.213; 0.064; 0.119), λmax=4.35; ИС=0.12; OC=0.13
WA=(0.127; 0.281; 0.120; 0.463), λmax=5.42; ИС=0.47; OC=0.52
WП=(0.721; 0.210; 0.069), λmax=4; ИС=0.33; OC=0.57
WЭ=(0.333; 0.333; 0.333), λmax=3; ИС=0.0; OC=0.0
WН=(0.713; 0.061; 0.176), λmax=3.11; ИС=0.06; OC=0.10
WЛ=(0.701; 0.097; 0.202; 0.463), λmax=3.14; ИС=0.07; OC=0.12
Осуществим иерархический синтез:
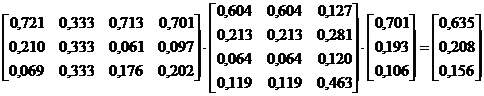
В приведенном примере некоторые матрицы несогласованные. Однако следует понимать, что человеку в данной ситуации нельзя было повторно задавать одни и те же вопросы до тех пор, пока все матрицы не стали бы однородными.
После решения задачи синтеза иерархии, оценивается однородность всей иерархии с помощью суммирования показателей однородности всех уровней, приведенных путем взвешивания к первому иерархическому уровню.