Аддитивная модель временного ряда

Назначение. С помощью данного сервиса производится построение аддитивной модели временного ряда:

Y = T + S + E

где T - трендовая составляющая, S - сезонная составляющая и E - случайная составляющая.

Укажите количество данных (количество строк), нажмите (Далее). Данные можно вставить из Word или Excel. На втором шаге выберите диапазон моделирования. Полученное решение сохраняется в файле MS Word и MS Excel (см. пример решения).

Скачать пример оформления

Алгоритм построения аддитивной модели

Построение аддитивной моделей сводится к расчету значений T, S и E для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.

Выравнивание исходного ряда методом скользящей средней.
Расчет значений сезонной компоненты S.
Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (T + E).
Аналитическое выравнивание уровней (T + E) с использованием полученного уравнения тренда.
Расчет полученных по модели значений (T + E).
Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок E для анализа взаимосвязи исходного ряда и других временных рядов.

Пример. Методику построения модели рассмотрим на примерах.
Имеются данные об объемах потребления электроэнергии (y_t) жителями региона за 16 кварталов.
Построить аддитивную модель временного ряда.

Решение.
Общий вид аддитивной модели следующий:
Y = T + S + E
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.
Рассчитаем компоненты аддитивной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Найдем скользящие средние (гр. 3 таблицы). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.2. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 4 табл.).

t	y_t	Скользящая средняя	Центрированная скользящая средняя	Оценка сезонной компоненты
1	375	-	-	-
2	371	657.5	-	-
3	869	653	655.25	213.75
4	1015	678	665.5	349.5
5	357	708.75	693.38	-336.38
6	471	710	709.38	-238.38
7	992	718.25	714.13	277.88
8	1020	689.25	703.75	316.25
9	390	689.25	689.25	-299.25
10	355	660.5	674.88	-319.88
11	992	678.25	669.38	322.63
12	905	703	690.63	214.38
13	461	685	694	-233
14	454	690.5	687.75	-233.75
15	920	-	-	-
16	927	-	-	-

Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 5 табл.). Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты S_i. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.

Показатели	1	2	3	4
1	-	-	213.75	349.5
2	-336.38	-238.38	277.88	316.25
3	-299.25	-319.88	322.63	214.38
4	-233	-233.75	-	-
Всего за период	-868.63	-792	814.25	880.13
Средняя оценка сезонной компоненты	-289.54	-264	271.42	293.38
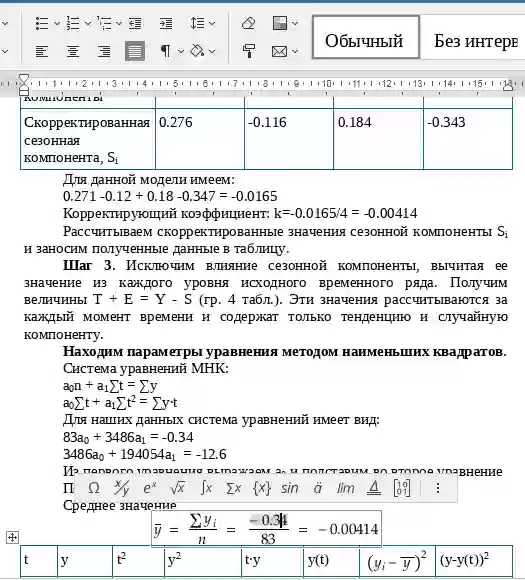
Скорректированная сезонная компонента, S_i	-292.35	-266.81	268.6	290.56

Для данной модели имеем:
-289.542 -264 + 271.417 + 293.375 = 11.25
Корректирующий коэффициент: k=11.25/4 = 2.812
Рассчитываем скорректированные значения сезонной компоненты S_i и заносим полученные данные в таблицу.
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины T + E = Y - S (гр. 4 табл.). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a₀n + a₁∑t = ∑y
a₀∑t + a₁∑t² = ∑y•t
Для наших данных система уравнений имеет вид:
16a₀ + 136a₁ = 10874
136a₀ + 1496a₁ = 92743.67
Из первого уравнения выражаем а₀ и подставим во второе уравнение
Получаем a₀ = 0.93, a₁ = 671.76
Среднее значения
y = 10874/16 = 679.63.

t	y	t²	y²	t•y	y(t)	(y-y_cp)²	(y-y(t))²
1	667.35	1	445361.58	667.35	672.68	150.57	28.41
2	637.81	4	406804.79	1275.63	673.61	1748.29	1281.41
3	600.4	9	360475.16	1801.19	674.53	6277.26	5496.59
4	724.44	16	524809.69	2897.75	675.46	2008.16	2398.77
5	649.35	25	421660.83	3246.77	676.39	916.32	730.71
6	737.81	36	544367.29	4426.88	677.31	3385.79	3660.4
7	723.4	49	523301.53	5063.77	678.24	1915.89	2039.34
8	729.44	64	532079.07	5835.5	679.16	2481.29	2527.6
9	682.35	81	465607.21	6141.19	680.09	7.45	5.14
10	621.81	100	386650.79	6218.13	681.01	3342.29	3504.73
11	723.4	121	523301.53	7957.35	681.94	1915.89	1718.69
12	614.44	144	377533.44	7373.25	682.86	4249.41	4682.22
13	753.35	169	567542.5	9793.6	683.79	5435.99	4839.21
14	720.81	196	519570.66	10091.38	684.72	1696.41	1303.02
15	651.4	225	424316.53	9770.94	685.64	796.89	1172.71
16	636.44	256	405052.69	10183	686.57	1865.16	2512.88
136	10874	1496	7428435.28	92743.67	10874	38193.03	37901.81

Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
T = 671.758 + 0.925t
Подставляя в это уравнение значения t = 1,...,16, найдем уровни T для каждого момента времени (гр. 5 табл.).

t	y_t	S_i	y_t - S_i	T	T + S_i	E = y_t - (T + S_i)	E²
1	375	-292.35	667.35	672.68	380.33	-5.33	28.41
2	371	-266.81	637.81	673.61	406.8	-35.8	1281.41
3	869	268.6	600.4	674.53	943.14	-74.14	5496.59
4	1015	290.56	724.44	675.46	966.02	48.98	2398.77
5	357	-292.35	649.35	676.39	384.03	-27.03	730.71
6	471	-266.81	737.81	677.31	410.5	60.5	3660.4
7	992	268.6	723.4	678.24	946.84	45.16	2039.34
8	1020	290.56	729.44	679.16	969.72	50.28	2527.6
9	390	-292.35	682.35	680.09	387.73	2.27	5.14
10	355	-266.81	621.81	681.01	414.2	-59.2	3504.73
11	992	268.6	723.4	681.94	950.54	41.46	1718.69
12	905	290.56	614.44	682.86	973.43	-68.43	4682.22
13	461	-292.35	753.35	683.79	391.44	69.56	4839.21
14	454	-266.81	720.81	684.72	417.9	36.1	1303.02
15	920	268.6	651.4	685.64	954.24	-34.24	1172.71
16	927	290.56	636.44	686.57	977.13	-50.13	2512.88

Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (гр. 6 табл.).
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
$R^{2} = 1 - {sum{}{}{}E^{2}}/{sum{}{}{}(y_{t} - overline{y})^{2}}$
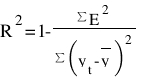
Среднее значения
y = 10874/16 = 679.63

t	y	(y-y_cp)²
1	375	92796.39
2	371	95249.39
3	869	35862.89
4	1015	112476.39
5	357	104086.89
6	471	43524.39
7	992	97578.14
8	1020	115855.14
9	390	83882.64
10	355	105381.39
11	992	97578.14
12	905	50793.89
13	461	47796.89
14	454	50906.64
15	920	57780.14
16	927	61194.39
136	10874	1496

R² = 1 - 37901.814/1252743.75 = 0.97
Следовательно, можно сказать, что аддитивная модель объясняет 97% общей вариации уровней временного ряда.
Шаг 6. Прогнозирование по аддитивной модели. Прогнозное значение F_t уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда:T = 671.758 + 0.925t
Получим
T₁₇ = 671.758 + 0.925*17 = 687.492
Значение сезонного компонента за соответствующий период равно: S₁ = -292.354
Таким образом, F₁₇ = T₁₇ + S₁ = 687.492 -292.354 = 395.137
T₁₈ = 671.758 + 0.925*18 = 688.417
Значение сезонного компонента за соответствующий период равно: S₂ = -266.813
Таким образом, F₁₈ = T₁₈ + S₂ = 688.417 -266.813 = 421.605
T₁₉ = 671.758 + 0.925*19 = 689.343
Значение сезонного компонента за соответствующий период равно: S₃ = 268.604
Таким образом, F₁₉ = T₁₉ + S₃ = 689.343 + 268.604 = 957.947
T₂₀ = 671.758 + 0.925*20 = 690.268
Значение сезонного компонента за соответствующий период равно: S₄ = 290.563
Таким образом, F₂₀ = T₂₀ + S₄ = 690.268 + 290.563 = 980.831

Аддитивная модель временного ряда

Алгоритм построения аддитивной модели

Правила ввода данных

Поиск

Процесс

Сообщение

Подключить услуги