Средний уровень моментного ряда
Для нахождения среднего значения моментного ряда с равностоящими уровнями используют среднюю хронологическую: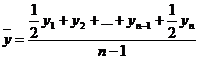
.
Средняя хронологическая для разностоящих уровней моментного ряда:
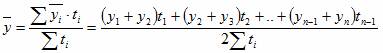
Назначение сервиса. С помощью данного онлайн калькулятора можно рассчитать среднее значение моментного ряда по формулам средней хронологической.
Пример №1. Численность населения города составила:
- на 1 января – 80500 человек,
- на 1 февраля – 80540 человек,
- на 1 марта – 80550 человек,
- на 1 апреля– 80560 человек,
- на 1 июля – 80620 человек,
- на 1 октября – 80680 человек,
- на 1 января следующего года – 80690 человек.
Решение.
Представленные данные - моментный ряд. Находим средние по формуле средней хронологической.
Средняя хронологическая для разностоящих уровней моментного ряда:
Средняя за I квартал:
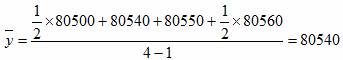человек
человек
Средняя за III квартал:
человек
Средняя за первое полугодие:
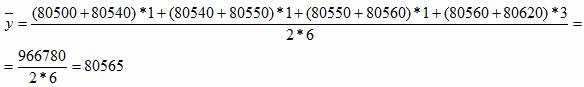человекПример №2. По данным Таблицы 7 (Приложение 2) выбрать динамический ряд, соответствующий Вашему варианту, для которого:
1. Рассчитать:
а) среднегодовой уровень ряда динамики;
б) цепные и базисные показатели динамики: абсолютный прирост, темп роста, темп прироста;
в) средний абсолютный прирост, средний темп роста, средний темп прироста.
Методические указания
Для характеристики динамики рассчитывают систему показателей динамики.
| Показатель динамики | Формулы расчета | |
| на цепной основе | на базисной основе | |
| Абсолютный прирост (+), сокращение (-) | Δц=yi-yi-1
| Δб=yi-y1
|
| Коэффициент роста | 
| 
|
| Темп роста | 
| 
|
| Темп прироста | Tпр ц = Tр ц - 100% | Tпр б = Tр б - 100% |
| Абсолютное значение одного процента прироста | A1%=0.01·yi-1
| - |
- средние уровни ряда;
- средние показатели изменения уровней ряда.
.
Для нахождения среднего уровня моментного ряда используют среднюю хронологическую:
.
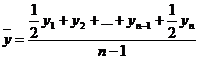Средний абсолютный прирост рассчитывается в зависимости от исходных данных следующими способами:
или 
Средний коэффициент роста (снижения):
или , 
.
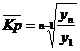Средний темп прироста (снижения): Tпр = Tр - 100%.
В следующем примере найдем средний размер фонда заработной платы (для интервального ряда).
| Год | Фонд заработной платы, тыс.руб. |
| 1994 | 300 |
| 1995 | 349 |
| 1996 | 379 |
| 1997 | 450 |
| 1998 | 501 |
| 1999 | 581 |
| 2000 | 600 |
| 2001 | 648 |
| 2002 | 677 |
| 2003 | 748 |
| 2004 | 800 |
Средний уровень интервального ряда рассчитывается по формуле:
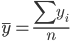
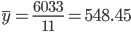
Средний размер ФЗП с 1994 по 2004 составил 548.45 тыс. руб.
Средний темп роста
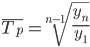
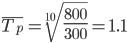
В среднем за весь период с 1994 по 2004 рост ФЗП составил 1.1 (ежегодно увеличивался на 10%).
Средний темп прироста
Tпр = Tр - 1 = 1.1-1 = 0.1
Средний абсолютный прирост
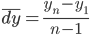
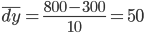
В среднем за весь период фонд заработной платы увеличивался на 50 тыс. руб. с каждым годом.
Более детальный анализ ФЗП.
В следующем примере найдем среднюю численность производственного персонала (для моментного ряда).
Цепные показатели ряда динамики.
| Период | численность ППП | Абсолютный прирост | Темп прироста, % | Темпы роста, % | Абсолютное содержание 1% прироста | Темп наращения, % |
| 1994 | 470 | 0 | 0 | 100 | 4.7 | 0 |
| 1995 | 500 | 30 | 6.38 | 106.38 | 4.7 | 6.38 |
| 1996 | 505 | 5 | 1 | 101 | 5 | 1.06 |
| 1997 | 533 | 28 | 5.54 | 105.54 | 5.05 | 5.96 |
| 1998 | 540 | 7 | 1.31 | 101.31 | 5.33 | 1.49 |
| 1999 | 589 | 49 | 9.07 | 109.07 | 5.4 | 10.43 |
| 2000 | 577 | -12 | -2.04 | 97.96 | 5.89 | -2.55 |
| 2001 | 594 | 17 | 2.95 | 102.95 | 5.77 | 3.62 |
| 2002 | 640 | 46 | 7.74 | 107.74 | 5.94 | 9.79 |
| 2003 | 628 | -12 | -1.88 | 98.13 | 6.4 | -2.55 |
| 2004 | 646 | 18 | 2.87 | 102.87 | 6.28 | 3.83 |
Для нахождения среднего уровня моментного ряда используют среднюю хронологическую:
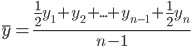
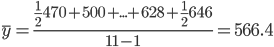
Средняя численность промышленного персонала предприятия за анализируемый период составила 566.4 чел.
см. также другие средние показатели ряда динамики.