Критерии продуктивности матрицы
Неотрицательная матрица A называется продуктивной, если существует такой положительный вектор x, для которого выполнено неравенство x>Ax.Критерии продуктивности матрицы А
Существует несколько критериев продуктивности матрицы А:
- Матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы.
- Для того чтобы обеспечить положительный конечный выпуск по всем отраслям необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:
- Определитель матрицы (E - A) не равен нулю, т.е. матрица (E- A) имеет обратную матрицу (E - A)-1.
- Наибольшее по модулю собственное значение матрицы А, т.е. решение уравнения |λE - A| = 0 строго меньше единицы.
- Все главные миноры матрицы (E - A) порядка от 1 до n, положительны.
Теорема. Для того чтобы линейная модель МОБ имела неотрицательное решение при любом ненулевом Y≥0 необходимо и достаточно, чтобы матрица прямых затрат A была продуктивной. Для продуктивной матрицы решение системы (1) единственное.
B = (E - A)-1
Критерии проверки продуктивности матрицы A.
- Первый критерий продуктивности. A – продуктивна тогда и только, когда существует B и B ≥ 0. Это означает, что матрица А продуктивна тогда и только тогда, когда матрица обратная матрица (Е - А)-1 существует и ее элементы неотрицательны.
- A ≥ 0 – продуктивна тогда и только, когда B имеет n положительных главных миноров.
Достаточные признаки продуктивности матрицы (Второй критерий продуктивности.):
- Сумма элементов в каждой строке меньше единицы.
- Сумма элементов в каждом столбце меньше единицы.
Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени. Взаимодействие отраслей определяется матрицей А прямых затрат. Задан вектор y объемом продуктов конечного потребления.
а) определить, является ли матрица продуктивной;
б) составить уравнение межотраслевого баланса;
в) найти объем валовой продукции каждой отрасли;
г) составить матрицу потоков средств производства;
Пример №1. Показать, что матрица 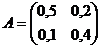 продуктивна.
продуктивна.
Решение. Приведем два способа проверки продуктивности матрицы.
1) используем условие λmax<1:
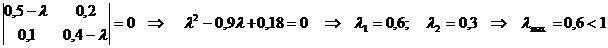
2) определим max
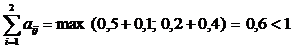 .
.
Следовательно, матрица A продуктивна.
Пример №2. Выяснить, продуктивна ли модель Леонтьева, заданная условиями: х1= 400, х2= 900, х11 =30, х12 =40, х21=70, х22 =120. Если модель продуктивна, то:
1) определить вектор-столбец конечного продукта У, соответствующий вектору-столбцу валового выпуска  ,
,
2) определить вектор-столбец валового выпуска Х, соответствующий, вектору-столбцу конечного продукта У = .
.
Решение.
1) Составим матрицу А и выясним, продуктивна ли она.
aij= → a11=
→ a11= ; a12=
; a12=
a21= ; a22=
; a22= →
→  → max (
→ max ( ) = max (
) = max ( ) = 0,25 < 1
) = 0,25 < 1
Следовательно, матрица A продуктивна.
2) Определим вектор-столбец У, соответствующий вектору-столбцу  : → У= (E - A)X =
: → У= (E - A)X = 
 =
=
 ;
;
3) Определим вектор-столбец Х, соответствующий вектору-столбцу У = : → X = (E - A)-1 У =
: → X = (E - A)-1 У =  =
=
Пример №3. Определить, будут ли следующие матрицы продуктивны.
Матрица A имеет неотрицательные элементы и удовлетворяет критерию продуктивности (при любом j сумма элементов столбца ∑aij ≤ 1.
I. Определим матрицу коэффициентов полных материальных затрат приближенно, учитывая косвенные затраты до 2-го порядка включительно.
а) Матрица коэффициентов косвенных затрат 1-го порядка равна:
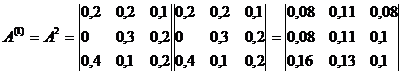
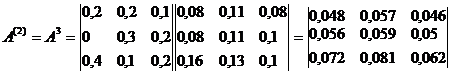
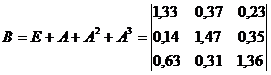
II. Определим матрицу коэффициентов полных затрат точно с помощью формул обращения невырожденных матриц.
Коэффициент полных затрат (bij) показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли.
Полные затраты отражают использование ресурса на всех этапах изготовления и равны сумме прямых и косвенных затрат на всех предыдущих стадиях производства продукции.
а) Находим матрицу (E-A):
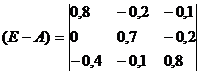
б) Вычисляем обратную матрицу (E-A)-1:
Запишем матрицу в виде:
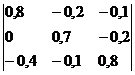
Главный определить
∆ = 0.8 • (0.7 • 0.8-(-0.1 • (-0.2)))-0 • (-0.2 • 0.8-(-0.1 • (-0.1)))+(-0.4 • (-0.2 • (-0.2)-0.7 • (-0.1))) = 0.388
Транспонированная матрица
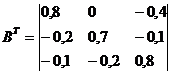
Алгебраические дополнения
∆1,1 = (0.7 • 0.8-(-0.2 • (-0.1))) = 0.54
∆1,2 = -(-0.2 • 0.8-(-0.1 • (-0.1))) = 0.17
∆1,3 = (-0.2 • (-0.2)-(-0.1 • 0.7)) = 0.11
∆2,1 = -(0 • 0.8-(-0.2 • (-0.4))) = 0.08
∆2,2 = (0.8 • 0.8-(-0.1 • (-0.4))) = 0.6
∆2,3 = -(0.8 • (-0.2)-(-0.1 • 0)) = 0.16
∆3,1 = (0 • (-0.1)-0.7 • (-0.4)) = 0.28
∆3,2 = -(0.8 • (-0.1)-(-0.2 • (-0.4))) = 0.16
∆3,3 = (0.8 • 0.7-(-0.2 • 0)) = 0.56
Обратная матрица
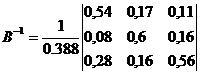
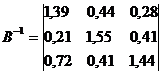
Найдем величины валовой продукции трех отраслей
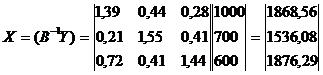
Составляющие третьего квадранта (условно-чистая продукция) находятся как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта.
Межотраслевой баланс состоит из четырех квадрантов (табл.). Первый квадрант отражает межотраслевые потоки продукции. Второй характеризует отраслевую материальную структуру национального дохода.
Третий представляет национальный доход как стоимость условно-чистой продукции (Zj), равной сумме амортизации (cj), оплаты труда (vj) и чистого дохода j-й отрасли (mj). Четвертый квадрант показывает конечное распределение и использование национального дохода.
| Производящие отрасли | Потребляющие отрасли | Конечный продукт | Валовый продукт | ||
| 1 | 2 | 3 | |||
| 1 | 373.71 | 307.22 | 187.63 | 1000 | 1868.56 |
| 2 | 0 | 460.82 | 375.26 | 700 | 1536.08 |
| 3 | 747.42 | 153.61 | 375.26 | 600 | 1876.29 |
| Чистый доход | 747.42 | 614.43 | 938.14 | 2300 | |
| Валовый продукт | 1868.56 | 1536.08 | 1876.29 | 5280.93 | |