Модель сезонной волны
Известна динамика реализации продовольственных товаров в магазинах города за 2001- 2004 гг., (данные приведены в таблице). Необходимо выявить и измерить сезонные колебания. Построить модель сезонной волны.| Кварталы | Годы | |||
| 2001 | 2002 | 2003 | 2004 | |
| I | 40 | 42 | 43 | 49 |
| II | 64 | 70 | 60 | 75 |
| III | 62 | 72 | 80 | 90 |
| IV | 50 | 44 | 53 | 64 |
Решение. Если в анализируемой временной последовательности наблюдаются устойчивые отклонения от тенденции (в большую или в меньшую сторону), то можно предположить наличие в ряду динамики некоторых (одного или нескольких) колебательных процессов.
Это особенно заметно, когда изучаемые явления имеют сезонный характер, — возрастание или убывание уровней повторяется регулярно с интервалом один год (например, производство молока и мяса по месяцам года, потребление топлива и электроэнергии для бытовых нужд, сезонная продажа товаров и т.д.).
Задачи, которые необходимо решить в ходе исследования сезонности:
1) выявить наличие сезонности;
2) численно выразить сезонные колебания;
3) выделить факторы, вызывающие сезонные колебания;
4) оценить последствия сезонных колебаний;
5) провести математическое моделирование сезонности.
Сезонность выявляется с помощью:
1) метода абсолютных разностей;
2) метода относительных разностей;
3) индексного метода.
Это особенно заметно, когда изучаемые явления имеют сезонный характер, — возрастание или убывание уровней повторяется регулярно с интервалом один год (например, производство молока и мяса по месяцам года, потребление топлива и электроэнергии для бытовых нужд, сезонная продажа товаров и т.д.).
Задачи, которые необходимо решить в ходе исследования сезонности:
1) выявить наличие сезонности;
2) численно выразить сезонные колебания;
3) выделить факторы, вызывающие сезонные колебания;
4) оценить последствия сезонных колебаний;
5) провести математическое моделирование сезонности.
Сезонность выявляется с помощью:
1) метода абсолютных разностей;
2) метода относительных разностей;
3) индексного метода.
Δc=yt-yc
где yt — средний месячный уровень показателя за три и более года,
yc — среднемесячное за все годы значение показателя.
Если сезонность оценивается по данным за три года (тридцать шесть месяцев), то
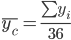
где yi — значение уровня динамического ряда.
Величина и знак значений абсолютных отклонений определяют наличие сезонности.
Метод относительных разностей является продолжением метода абсолютных разностей. В качестве показателя, характеризующего сезонную неравномерность, используется показатель относительного отклонения:
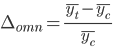
По величине и знакам значений относительных отклонений можно судить о величине и силе влияния сезонного фактора.
Индекс сезонности рассчитывается:
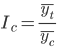
где yt — средний месячный уровень показателя за три и более года,
yc — среднемесячное за все годы значение показателя.
Расчет индекса сезонности по данной формуле не учитывает наличие тренда.
Рассчитанные значения индекса сезонности сравниваются со значением 100 %. Если индекс сезонности превышает 100 % — это свидетельствует о влиянии сезонного фактора в сторону увеличения уровней динамического ряда.
Если индекс сезонности меньше 100 % — то сезонный фактор вызывает снижение уровней динамического ряда.
Определим наличие сезонных колебаний для динамического ряда.
| Период | 1 | 2 | 3 | 4 | yt | Δсез | Δотн,% | Iсез, % |
| 1 | 40 | 42 | 43 | 49 | 43.5 | -16.38 | -27.35 | 72.65 |
| 2 | 64 | 70 | 60 | 75 | 67.25 | 7.38 | 12.32 | 112.32 |
| 3 | 62 | 72 | 80 | 90 | 76 | 16.13 | 26.93 | 126.93 |
| 4 | 50 | 44 | 53 | 64 | 52.75 | -7.13 | -11.9 | 88.1 |
| 59.88 |
Рисунок - Индексы сезонности