Алгоритм К-средних
Метод K-средних – это метод кластерного анализа, целью которого является разделение m наблюдений на k кластеров, при этом каждое наблюдение относится к тому кластеру, к центу (центроиду) которого оно ближе всего.Назначение. С помощью онлайн-калькулятора можно проводить классификацию объектов методом К-средних с построением дендрограммы (например, для построения типологической группировки).
Алгоритм разделительной кластеризации, основан на разбиении множества элементов векторного пространства на заранее определенное число кластеров k. Метод относится к неирархическим алгоритмам кластеризации. Алгоритм представляет собой итерационную процедуру:
- Выбирается число кластеров k.
- Из исходного множества данных случайным образом выбираются k записей, которые будут служить начальными центрами кластеров.
- Для каждой записи исходной выборки определяется ближайший к ней центр кластера. При этом записи, «притянутые» определенным центром, образуют начальные кластеры.
- Вычисляются центроиды – центры тяжести кластеров. Каждый центроид – это вектор, элементы которого представляют собой средние значения признаков, вычисленные по всем записям кластера. Затем центр кластера смещается в его центроид.
Достоинства алгоритма k-средних:
- простота реализации;
- интуитивная понятность и прозрачность алгоритма;
Недостатки алгоритма k-средних:
- число кластеров надо знать заранее;
- зависимость результата от инициализации центров кластеров;
- вычислительная сложность;
Пример №1. По данной выше таблице провести классификацию объектов на три класса методом К-средних. Провести максимальное число итераций. Эталонные точки и порядок появления точек задать самостоятельно. Отобразить на плоскости по лученный вариант классификации.
| Объекты | A | B | C | D | E | F |
| признак-X | –2 | –2 | –3 | 4 | 3 | 0 |
| признак-Y | 0 | –1 | 0 | 0 | 0 | 0 |
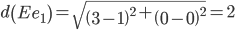
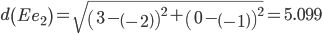
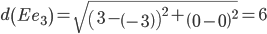
Минимальным является расстояние d(Ee1)
Пересчитываем значения для эталонной точки e1: (3+1)/2 = 2;(0+0)/2 = 0;
Сравниваем расстояние от точки F до эталонных точек.
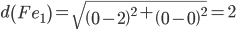
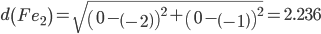
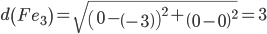
Минимальным является расстояние d(Fe1)
Пересчитываем значения для эталонной точки e1: (0+2)/2 = 1;(0+0)/2 = 0;
Произведём классификацию объектов:
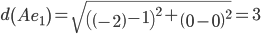
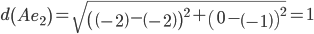
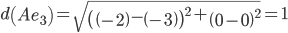
Объект A ближе всех расположен к эталонной точке e2.
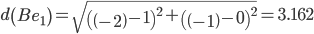
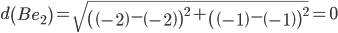
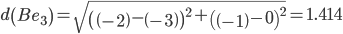
Объект B ближе всех расположен к эталонной точке e2.
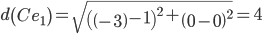
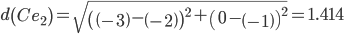
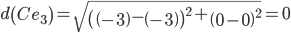
Объект C ближе всех расположен к эталонной точке e3.
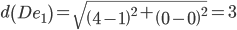
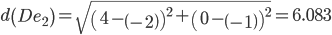
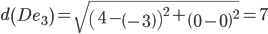
Объект D ближе всех расположен к эталонной точке e1.
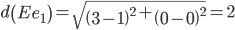
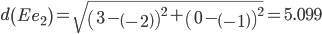
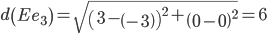
Объект E ближе всех расположен к эталонной точке e1.
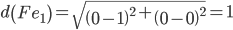
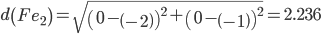
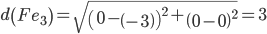
Объект F ближе всех расположен к эталонной точке e1.
| e1 | e2 | e3 |
| DEF | AB | C |
Сравниваем расстояние от точки A до эталонных точек.
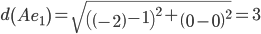
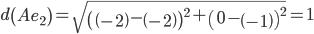
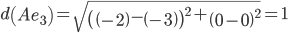
Минимальным является расстояние d(Ae2)
Пересчитываем значения для эталонной точки e2: (-2+(-2))/2 = -2;(0+(-1))/2 = -0.5;
Сравниваем расстояние от точки B до эталонных точек.
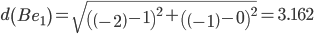
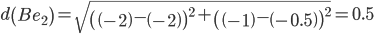
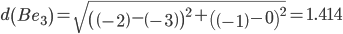
Минимальным является расстояние d(Be2)
Пересчитываем значения для эталонной точки e2: (-2+(-2))/2 = -2;(-1+(-0.5))/2 = -0.75;
Сравниваем расстояние от точки D до эталонных точек.
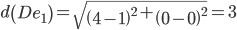
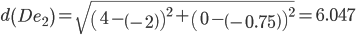
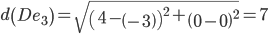
Минимальным является расстояние d(De1)
Пересчитываем значения для эталонной точки e1: (4+1)/2 = 2.5;(0+0)/2 = 0;
Сравниваем расстояние от точки E до эталонных точек.
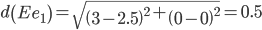
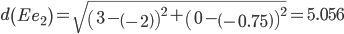
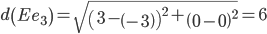
Минимальным является расстояние d(Ee1)
Пересчитываем значения для эталонной точки e1: (3+2.5)/2 = 2.75;(0+0)/2 = 0;
Сравниваем расстояние от точки F до эталонных точек.
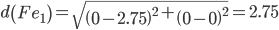
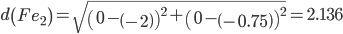
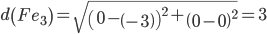
Минимальным является расстояние d(Fe2)
Пересчитываем значения для эталонной точки e2: (0+(-2))/2 = -1;(0+(-0.75))/2 = -0.375;
Произведём классификацию объектов:
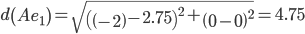
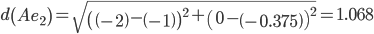
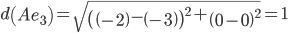
Объект A ближе всех расположен к эталонной точке e3.
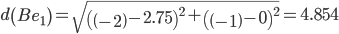
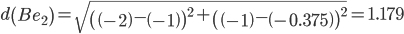
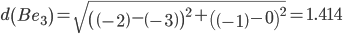
Объект B ближе всех расположен к эталонной точке e2.
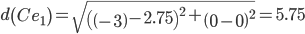
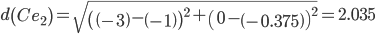
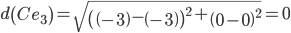
Объект C ближе всех расположен к эталонной точке e3.
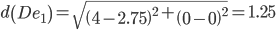
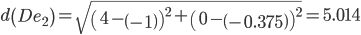
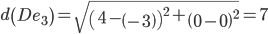
Объект D ближе всех расположен к эталонной точке e1.
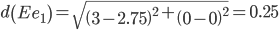
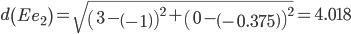
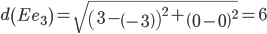
Объект E ближе всех расположен к эталонной точке e1.
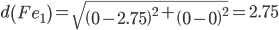
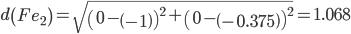
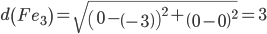
Объект F ближе всех расположен к эталонной точке e2.
| e1 | e2 | e3 |
| DE | BF | AC |
Итерация №2
Сравниваем расстояние от точки A до эталонных точек.
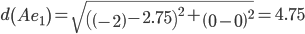
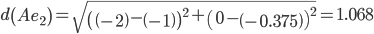
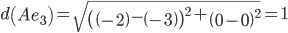
Минимальным является расстояние d(Ae3)
Пересчитываем значения для эталонной точки e3: (-2+(-3))/2 = -2.5;(0+0)/2 = 0;
Сравниваем расстояние от точки B до эталонных точек.
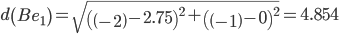
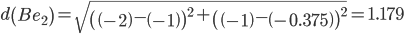
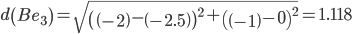
Минимальным является расстояние d(Be3)
Пересчитываем значения для эталонной точки e3: (-2+(-2.5))/2 = -2.25;(-1+0)/2 = -0.5;
Сравниваем расстояние от точки C до эталонных точек.
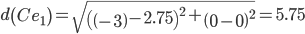
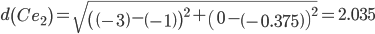
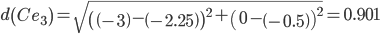
Минимальным является расстояние d(Ce3)
Пересчитываем значения для эталонной точки e3: (-3+(-2.25))/2 = -2.625;(0+(-0.5))/2 = -0.25;
Сравниваем расстояние от точки D до эталонных точек.
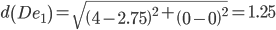
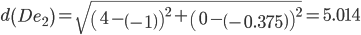
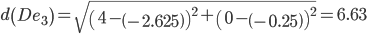
Минимальным является расстояние d(De1)
Пересчитываем значения для эталонной точки e1: (4+2.75)/2 = 3.375;(0+0)/2 = 0;
Сравниваем расстояние от точки E до эталонных точек.
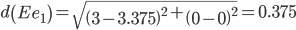
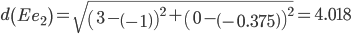
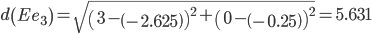
Минимальным является расстояние d(Ee1)
Пересчитываем значения для эталонной точки e1: (3+3.375)/2 = 3.1875;(0+0)/2 = 0;
Сравниваем расстояние от точки F до эталонных точек.
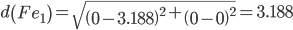
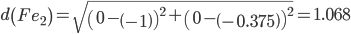
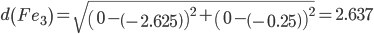
Минимальным является расстояние d(Fe2)
Пересчитываем значения для эталонной точки e2: (0+(-1))/2 = -0.5;(0+(-0.375))/2 = -0.1875;
Произведём классификацию объектов:
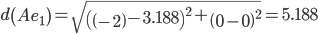
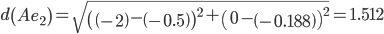
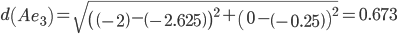
Объект A ближе всех расположен к эталонной точке e3.
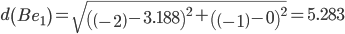
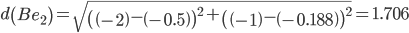
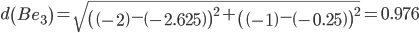
Объект B ближе всех расположен к эталонной точке e3.
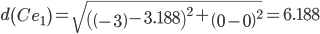
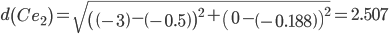
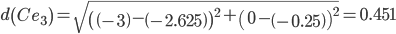
Объект C ближе всех расположен к эталонной точке e3.
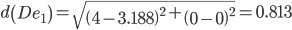
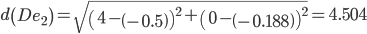
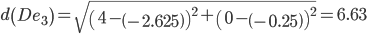
Объект D ближе всех расположен к эталонной точке e1.
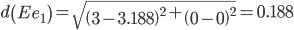
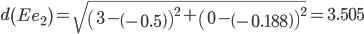
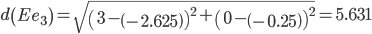
Объект E ближе всех расположен к эталонной точке e1.
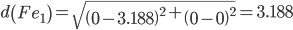
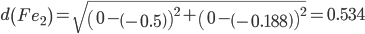
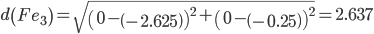
Объект F ближе всех расположен к эталонной точке e2.
| e1 | e2 | e3 |
| DE | F | ABC |
Итерация №3
Сравниваем расстояние от точки A до эталонных точек.
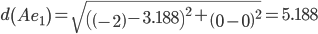
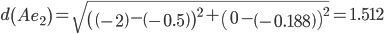
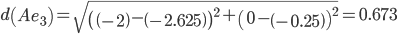
Минимальным является расстояние d(Ae3)
Пересчитываем значения для эталонной точки e3: (-2+(-2.625))/2 = -2.3125;(0+(-0.25))/2 = -0.125;
Сравниваем расстояние от точки B до эталонных точек.
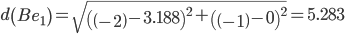
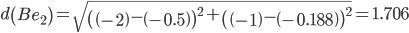
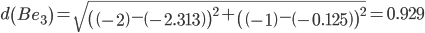
Минимальным является расстояние d(Be3)
Пересчитываем значения для эталонной точки e3: (-2+(-2.3125))/2 = -2.15625;(-1+(-0.125))/2 = -0.5625;
Сравниваем расстояние от точки C до эталонных точек.
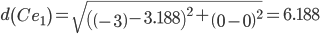
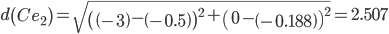
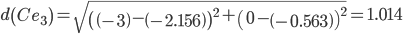
Минимальным является расстояние d(Ce3)
Пересчитываем значения для эталонной точки e3: (-3+(-2.15625))/2 = -2.578125;(0+(-0.5625))/2 = -0.28125;
Сравниваем расстояние от точки D до эталонных точек.
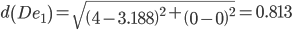
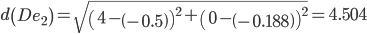
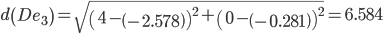
Минимальным является расстояние d(De1)
Пересчитываем значения для эталонной точки e1: (4+3.1875)/2 = 3.59375;(0+0)/2 = 0;
Сравниваем расстояние от точки E до эталонных точек.
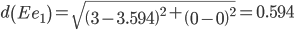
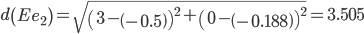
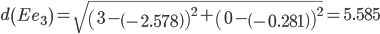
Минимальным является расстояние d(Ee1)
Пересчитываем значения для эталонной точки e1: (3+3.59375)/2 = 3.296875;(0+0)/2 = 0;
Сравниваем расстояние от точки F до эталонных точек.
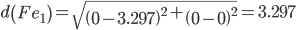
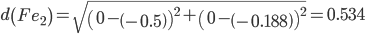
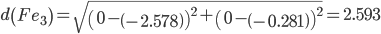
Минимальным является расстояние d(Fe2)
Пересчитываем значения для эталонной точки e2: (0+(-0.5))/2 = -0.25;(0+(-0.1875))/2 = -0.09375;
Произведём классификацию объектов:
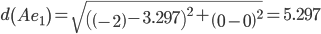
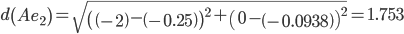
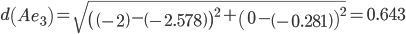
Объект A ближе всех расположен к эталонной точке e3.
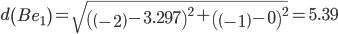
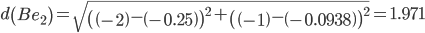
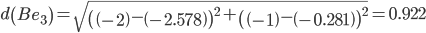
Объект B ближе всех расположен к эталонной точке e3.
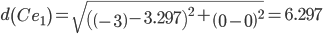
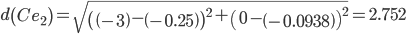
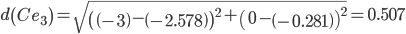
Объект C ближе всех расположен к эталонной точке e3.
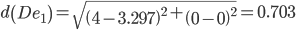
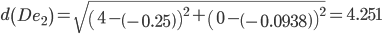
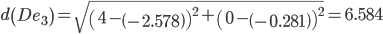
Объект D ближе всех расположен к эталонной точке e1.
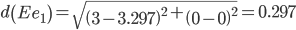
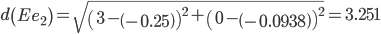
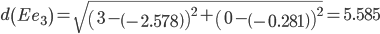
Объект E ближе всех расположен к эталонной точке e1.
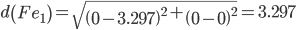
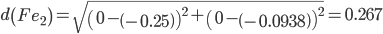
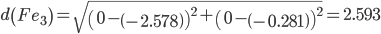
Объект F ближе всех расположен к эталонной точке e2.
| e1 | e2 | e3 |
| DE | F | ABC |
Пример №2. Даны четыре объекта, каждый определяется двумя признаками. Разбить объекты на три кластера методом k-средних. Первоначально первые три объекта образуют начальные кластеры, метрика – квадрат евклидова расстояния: X1(2;3), Х2(3;2), Х3(7;3), Х4 (5;-3).