Конкурентный анализ при помощи кривой Лоренца
Задание. Построить кривые Лоренца для каждого временного интервала и проанализировать их.
| Группы по денежным доходам, % | Доля денежных доходов в группе, % |
| 20 | 5.3 |
| 40 | 10 |
| 60 | 15 |
| 80 | 22.6 |
| 100 | 47.1 |
Решение.
Решение проводим, используя сервис Кривая Лоренца онлайн
Линия фактического неравенства строится на основании данных о процентах дохода приходящихся на каждые 20 % населения.
Если нижняя первая часть фирм получила 5.3% всех доходов, то графически это будет точка А. Чтобы получить точку В необходимо сложить процент дохода первых 20 % фирм с процентами доходов вторых 20 % фирма (5.3% + 10%) и т.д.
| 20-ти процентные группы фирм | Объем денежных доходов, в % к итогу | Доля денежных доходов нарастающим итогом, % | Площадь треугольника | Площадь прямоугольника | Общая площадь фигуры, Si |
| 20 | 5.3 | 5.3 | 53 | 0 | 53 |
| 40 | 10 | 15.3 | 100 | 53 | 153 |
| 60 | 15 | 30.3 | 150 | 153 | 303 |
| 80 | 22.6 | 52.9 | 226 | 303 | 529 |
| 100 | 47.1 | 100 | 471 | 529 | 1000 |
| 2038 |
1. Рассчитаем коэффициенты концентрации доходов (индекс Джини).
Коэффициент концентрации доходов (индекс Джини) представляет собой отношение площади фигуры, образованной кривой Лоренца и линией абсолютного равенства (S1) к площади всего треугольника OGE. Для приблизительной оценки коэффициента Джини отрезки кривой Лоренца представляют в виде прямых линий OA, AB, BC, CD, DE. Затем последовательно находят площади треугольников и прямоугольников и получают площадь фигуры S2. Чем больше индекс Джини, тем больше неравенство.
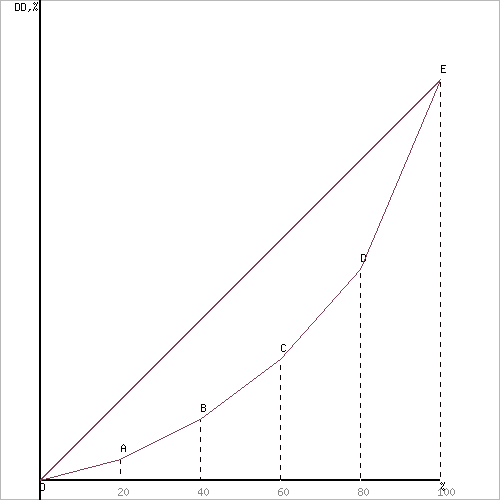
Таким образом, уровень неравенства определяется с помощью коэффициента Джини.
Он рассчитывается как отношение площади фигуры OABCDE к площади треугольника OEG. Для того чтобы определить площадь фигуры, лежащей ниже кривой Лоренца, соединяем прямыми линиями точки ОА, АВ и т.д.
Опускаем перпендикуляр на ось X и находим площади фигур, лежащих ниже точек А, B, С.
SOAA\' = 1/2•10%•5.3
Площадь SABB\'A состоит из треугольника и прямоугольника. Фигура BCCB\' также состоит из треугольника и прямоугольника.
Сложив все площади фигур, получим площадь фигуры S2.
Площадь треугольника OEG находим по формуле:
1/2•100%•100% = 5000
Отсюда коэффициент Лоренца равен:
(SOEG - S2) / SOEG
(5000 - 2038) / 5000 = 0.592
2. Индекс Джини.
Для исчисления коэффициента Джини необходимо рассчитать величины pi и qi. Здесь qi - это площадь фигуры Si деленная на 1000.
| pi | qi | piqi+1 | pi+1qi |
| 0.2 | 0.053 | 0.0306 | - |
| 0.4 | 0.15 | 0.12 | 0.0212 |
| 0.6 | 0.3 | 0.32 | 0.0918 |
| 0.8 | 0.53 | 0.8 | 0.24 |
| 1 | 1 | - | 0.53 |
| ВСЕГО | 0 | 1.27 | 0.88 |
Коэффициент Джини равен:
KL = ∆piqi+1 - ∆pi+1qi = 1.2692 - 0.8844 = 0.3848