Функция полезности. Пример решения
Пример №1. Решите задачу потребительского выбора, найдя функции спроса, при ценах благ p1=5, p2=1 и доходе I=40, со следующей функцией полезности U=(x1-1)1/2*(x2-6)3/4 → max.
Решение осуществляем с помощью калькулятора
U = (x1-1)1/2•(x2-6)3/4
Вектор цен равен Р = (5; 1); величина дохода равна 40.
Предельные полезности имеют вид:
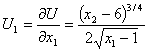
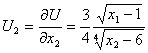
D = 40
Необходимые условия оптимума дают следующую систему уравнений (λ — множитель Лагранжа):
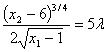

5x1 + x2 = 40
После подстановки первого уравнения во второе получим:

Выразив из третьего уравнения x1 и подставив в последнее равенство, будем иметь:
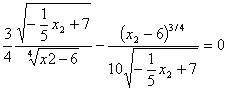
Решая его относительно x2 получим: x2 = 117/5
При x2 = 117/5: x1 = 83/25
Точка спроса: (83/25; 117/5).
Чтобы найти функции спроса x1 = f(I), x2 = f(I), аналогично составляем систему уравнений:
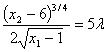

5x1 + x2 = I
Решая ее, получаем:
x1 = 1/25(2I+3)
x2 = 3/5(I-1)
Оптимальный потребительский набор. Для двух товаров целевая функция потребления имеет вид:
U = (x1-1)1/2•(x2-6)3/4
Вектор цен равен Р = (5; 1); величина дохода равна 40.
Предельные полезности имеют вид:
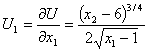
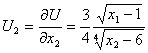
D = 40
Необходимые условия оптимума дают следующую систему уравнений (λ — множитель Лагранжа):
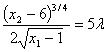

5x1 + x2 = 40
После подстановки первого уравнения во второе получим:

Выразив из третьего уравнения x1 и подставив в последнее равенство, будем иметь:
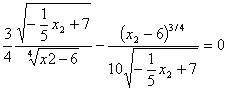
Решая его относительно x2 получим: x2 = 117/5
При x2 = 117/5: x1 = 83/25
Точка спроса: (83/25; 117/5).
Чтобы найти функции спроса x1 = f(I), x2 = f(I), аналогично составляем систему уравнений:
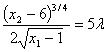

5x1 + x2 = I
Решая ее, получаем:
x1 = 1/25(2I+3)
x2 = 3/5(I-1)
Пример №2. Найдите оптимальный потребительский набор, если функция предпочтений потребителя u(x1,x2)=(x1-4)1/4(x2-10)3/4, цены первого и второго товара соответственно 25 и 10 ден. ед., доход потребителя 400 ден.ед.
Для решения, используем функцию спроса модели Стоуна: 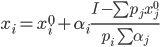
В нашем случае: x10 = 4; x20 = 10; α1 = 1/4; α2 = 3/4
Используя формулу, получаем: x1 = 4 + 1/4 • (400 - 25 • 4 - 10 • 10)/(25(1/4 + 3/4)) = 6
x2 = 10 + 3/4 • (400 - 25 • 4 - 10 • 10)/(10(1/4 + 3/4)) = 25
Откуда: Umax = (6-4)1/4(25-10)3/4 = 9.06412613