Функция полезности Стоуна
Функция спроса для конкретной функции потребительского предпочтения называется функцией Р.Стоуна и имеет вид:Модель Стоуна
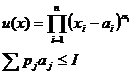
где pj – цена j-го блага, I – доход (бюджет).
Функция полезности U в модели Стоуна характеризуется минимальным объемом потребления x10 , x20 и коэффициентом полезности для каждого из товаров a1 и a2, соответственно.
С учетом бюджетного ограничения, функция спроса имеет вид:
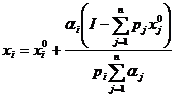
Пример. Решите задачу потребительского выбора, найдя функции спроса, при ценах благ p1=7, p2=3 и доходе I=55, со следующими функциями полезности:
U=(x1-1)3/4×(x2 –3)1/3 → max
Изобразите допустимое множество и кривые безразличия.
1. Решение через функцию Лагранжа
Для двух товаров целевая функция потребления имеет вид:
U = (x1-1)3/4•(x2-3)1/3
Вектор цен равен Р = (7; 3); величина дохода равна 55.
Предельные полезности имеют вид:
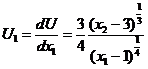
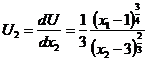
D = 55
Необходимые условия оптимума дают следующую систему уравнений (λ — множитель Лагранжа):
3/4•((x2-3)1/3)/((x1-1)1/4) = 7λ
((x1-1)3/4)/(3•(x2-3)2/3) = 3λ
7x1 + 3x2 = 55
После подстановки первого уравнения во второе получим:
((x1-1)3/4)/(3•(x2-3)2/3) = 3*(3/4•((x2-3)1/3)/((x1-1)1/4))/7
Выразив из третьего уравнения x1 и подставив в последнее равенство, будем иметь:
((-3/7•x2+48/7)3/4)/(3•(x2-3)2/3)-9/28•((x2-3)1/3)/((-3/7•x2+48/7)1/4) = 0
Решая его относительно x2 получим:
x2 = 7
При x2 = 7
x1 = 34/7 или x1 = 4,857
U(X) = 18/72/3•(21)1/4 или U(X) = 4.018
Для двух товаров целевая функция потребления имеет вид:
U = (x1-1)3/4•(x2-3)1/3
Вектор цен равен Р = (7; 3); величина дохода равна 55.
Предельные полезности имеют вид:
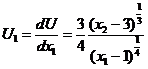
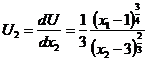
D = 55
Необходимые условия оптимума дают следующую систему уравнений (λ — множитель Лагранжа):
3/4•((x2-3)1/3)/((x1-1)1/4) = 7λ
((x1-1)3/4)/(3•(x2-3)2/3) = 3λ
7x1 + 3x2 = 55
После подстановки первого уравнения во второе получим:
((x1-1)3/4)/(3•(x2-3)2/3) = 3*(3/4•((x2-3)1/3)/((x1-1)1/4))/7
Выразив из третьего уравнения x1 и подставив в последнее равенство, будем иметь:
((-3/7•x2+48/7)3/4)/(3•(x2-3)2/3)-9/28•((x2-3)1/3)/((-3/7•x2+48/7)1/4) = 0
Решая его относительно x2 получим:
x2 = 7
При x2 = 7
x1 = 34/7 или x1 = 4,857
U(X) = 18/72/3•(21)1/4 или U(X) = 4.018
В нашем случае x10 =1, x20=3, α1=3/4 и α2=1/3.
Используя калькулятор, получаем:
x1= 1+0,75*(55-7*1-3*3)/(7*(0,75+0,33)) = 4,8690
x2= 3+0,33*(55-7*1-3*3)/(3*(0,75+0,33)) = 6.9722.
(4.8690-1)3/4(6.9722-3)1/3 = 4.36894
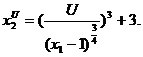
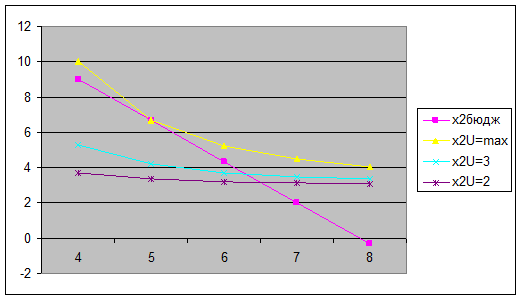
Далее составим таблицу с допустимым множеством значений и построим кривые безразличия и прямую бюджетного ограничения.
| x1 | 4 | 5 | 6 | 7 | 8 |
| x2бюдж | 9 | 6,666667 | 4,333333 | 2 | -0,33333 |
| x2U=max | 10,04053 | 6,685473 | 5,230723 | 4,480089 | 4,046303 |
| x2U=3 | 5,279507 | 4,193243 | 3,72224 | 3,479207 | 3,338761 |
| x2U=2 | 3,675409 | 3,353553 | 3,213997 | 3,141987 | 3,100374 |
| Umax | 4,36894 | ||||
| U1 | 3 | ||||
| U2 | 2 |
Задача 2.
Решите задачу потребительского выбора, найдя функции спроса, при ценах благ p1=5, p2=1 и доходе I=40, со следующими функциями полезности:
U=(x1-1)1/2(x2-6)3/4 → max
Решение.