Оптимальный размер заказа. Примеры решений

Пример №1. Магазин ежедневно продает Q телевизоров. Накладные расходы на поставку партии телевизоров в магазин оцениваются в S руб. Стоимость хранения одного телевизора на складе магазина составляет s руб. Определить оптимальный объем партии телевизоров, оптимальные среднесуточные издержки на хранение и пополнение запасов телевизоров на складе. Чему будут равны эти издержки при объемах партий n1 и n2 телевизоров?
Скачать решение.

Решение проводится с помощью онлайн-калькулятора Оптимальный размер заказа.

Пример №2. Рассчитать оптимальный размер заказа для всех комплектующих изделий, по формуле Вильсона (c1=12;c2=0.3;q=1).Пример №2
(c1=5;c2=0.1;q=150).Пример №3

Пример №3. Интенсивность спроса составляет 1000 единиц товара в год. Организационный издержки равны 7 у.е., издержки на хранение - 6 у.е., цена единица товара - 6 у.е. Определить оптимальный размер партии, число партий за год, интервал между поставками и общие издержки. Построить график запасов.
Скачать решение

Пример №4. Рассмотрите все этапы решения задачи об оптимальном размере закупаемой партии товара при следующих данных: Q=72, C₀ = 3 тыс.р/м, C₁ = 400 р/м, C₂ = 100 р/м.
Скачать решение

Пример №5. Годовой спрос на вентили стоимостью $4 за штуку равен 1000 единиц. Затраты хранения оцениваются в 10% от стоимости каждого изделия. Средняя стоимость заказа составляет $ 1,6 за заказ. В году 270 рабочих дней. Определите размер экономического заказа. Определите оптимальное число дней между заказами.
Решение: Скачать решение

Пример №6. На склад доставляется зерно партиями по 800 тонн. Расход зерна со склада составляет в сутки 200 тонн. Накладные расходы по доставке партии зерна равны 1,5 млн. руб. Издержки хранения 1 тонны зерна в течение суток составляют 80 руб.
Требуется определить:

• длительность цикла, среднесуточные накладные расходы и среднесуточные издержки хранения;
• оптимальный размер заказываемой партии и расчетные характеристики работы склада в оптимальном режиме;

Оптимальный размер заказа рассчитывается по формуле Вильсона: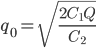
где q₀ – оптимальный размер заказа, шт.;
С₁ = 1500000, стоимость выполнения одного заказа, руб.;
Q = 200, потребность в товарно-материальных ценностях за определенный период времени (год), шт.;
C₂ = 80, затраты на содержание единицы запаса, руб./шт.
т
Оптимальный средний уровень запаса: 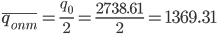т
Оптимальная периодичность пополнения запасов: 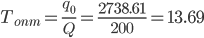дней

Пример №7. Годовой спрос D единиц, стоимость подачи заказа C₀ рублей/заказ, закупочная цена C_b рублей/единицу, годовая стоимость хранения одной единицы составляет a% ее цены. Время доставки 6 дней, 1 год = 300 рабочих дней. Найти оптимальный размер заказа, издержки, уровень повторного заказа, число циклов за год, расстояние между циклами. Можно получить скидку b% у поставщиков, если размер заказа будет не меньше d единиц. Стоит ли воспользоваться скидкой? Годовая стоимость отсутствия запасов C_d рублей/единицу. Сравнить 2 модели: основную и с дефицитом (заявки выполняются).

Решение получаем с помощью калькулятора. Предварительно находим стоимость хранения одной единицы, C₂ = 40*20% = 8 руб. (вводится в основную модель) и при скидке, C₂ = (1-0.03)*40*20% = 7.76 руб. (для модели со скидкой)

1. Расчет оптимального размера заказа.
Оптимальный размер заказа рассчитывается по формуле Вильсона: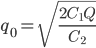
где q₀ – оптимальный размер заказа, шт.;
С₁ = 50, стоимость выполнения одного заказа, руб.;
Q = 400, потребность в товарно-материальных ценностях за определенный период времени (год), шт.;
C₂ = 8, затраты на содержание единицы запаса, руб./шт.

Оптимальный средний уровень запаса: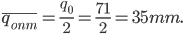
Оптимальная периодичность пополнения запасов: 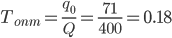(год) или 0.18·300=53 дня.

2. Интервал времени между заказами при условии соблюдения оптимальной партии поставки.

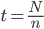
где N - количество рабочих дней в году; n – количество партий поставок за период (год);

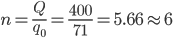
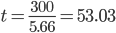дней
Точка заказа: 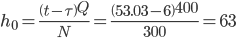шт.

3. Общегодовые издержки по складу за год составят: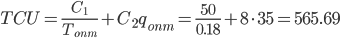
Общие издержки
TC = p · Q + TCU = 40 · 400 + 565.69 = 16565.69 руб./год
Если воспользоваться скидкой, оптимальный размер заказа равен:
Но скидка предоставляется, если объем заказа q ≥ 80, поэтому положим q = 80.
Тогда издержки по складу равны: 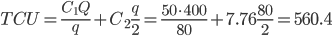руб./год
Общие издержки: TC = (1-0.03)*40 · 400 + 560.4 = 16080.4 руб./год
Общие издержки уменьшились. Поэтому следует воспользоваться скидкой, заказывая каждый раз 80 единиц.
Интервал между циклами: 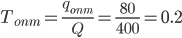год или 0.2 · 300=60 дней.
Число циклов за год: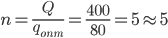

4. Модель с дефицитом.
Оптимальный размер заказа рассчитывается по формуле: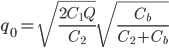
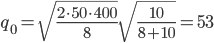ед.
Максимальный размер дефицита.
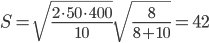ед.
Общегодовые издержки по складу за год составят: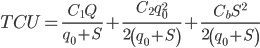
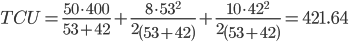руб./год.
Таким образом, в модели с дефицитом годовые издержки меньше.