Оптимальный размер заказа по формуле Вильсона
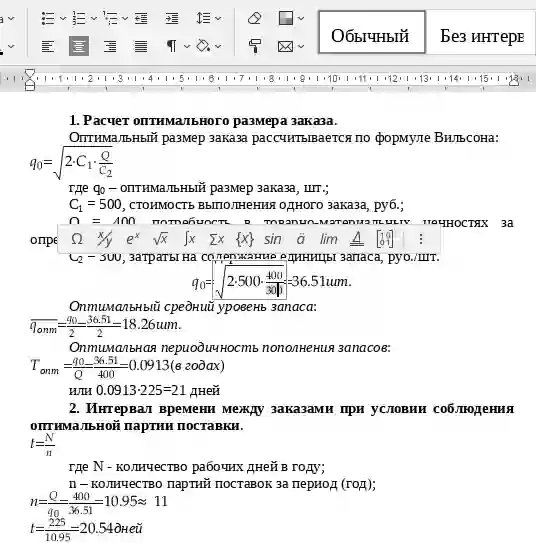
Оптимальный размер заказа рассчитывается по формуле Уилсона:где q0 – оптимальный размер заказа, шт.;
С1 – стоимость выполнения одного заказа, руб. (накладные расходы);
Q – потребность в товарно-материальных ценностях за определенный период времени (год), шт.;
C2 – затраты на содержание единицы запаса, руб./шт.
Назначение сервиса. Сервис предназначен для расчета параметров системы управления запасами:
- с фиксированным размером заказа;
- с фиксированным интервалом времени между заказами.
Свойства формулы Вильсона
Размер партии q0 оптимален тогда и только тогда, когда издержки хранения за время цикла Т равны накладным расходам C1.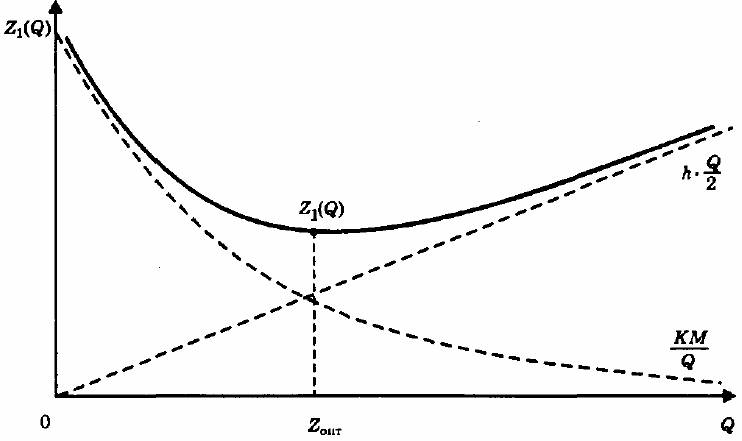
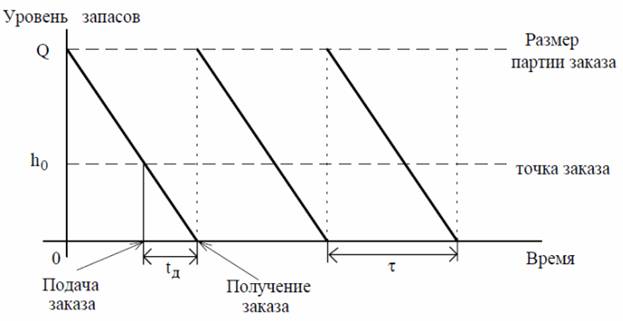
Модель экономически выгодных размеров заказываемых партий
Моделирование работы склада обычно делаются следующие предположения:- скорость расходования запасов со склада — постоянная величина, которую обозначим М (единиц товарных запасов в единицу времени); в соответствии с этим график изменения величины запасов в части расходования является отрезком прямой;
- объем партии пополнения Q есть постоянная величина, так что система управления запасами — это система с фиксированным размером заказа;;
- время разгрузки прибывшей партии пополнения запасов мало, будем считать его равным нулю;
- время от принятия решения о пополнении до прихода заказанной партии есть постоянная величина Δt, так что можно считать, что заказанная партия приходит как бы мгновенно: если нужно, чтобы она пришла точно в определенный момент, то ее следует заказать в момент времени на Δt ранее;
- на складе не происходит систематического накопления или перерасхода запасов. Если через Т обозначить время между двумя последовательными поставками, то обязательно выполнение равенства: Q = МТ. Из сказанного выше следует, что работа склада происходит одинаковыми циклами длительностью Т, и за время цикла величина запаса изменяется от максимального уровня S до минимального уровня s;
- считается обязательным выполнение требования, чтобы отсутствие запасов на складе было недопустимым, т.е. выполняется неравенство s ≥ 0. С точки зрения уменьшения издержек склада на хранение отсюда вытекает, что s = 0 и, следовательно, S = Q.
Пример №1. Годовая потребность в сырье составляет 125 тыс.кг., затраты на размещение и выполнение одного заказа 2500 руб., затраты на хранение одного кг. сырья 250 руб. в год, цена 1 кг. сырья – 5 руб. Определите оптимальный размер поставки, количество поставок, интервал между поставками и стоимость 1 поставки.
Решение: здесь C1 = 2500, C2=250, Q = 125 000
Пример №2. Химическое предприятие производит бисульфат соды в упаковках по 50 кг. Спрос на этот товар - 20 тонн в день. Существующие мощности позволяют производить по 50 тонн в день. Стоимость наладки оборудования $100, стоимость хранения и погрузочных работ - $5 за тонну в год. Предприятие работает 200 дней в году.
Какое количество упаковок оптимально для производственного цикла? Каким будет средний уровень запасов для данного объема производственной партии? Какова примерная продолжительность производственного цикла? Сколько производственных циклов будет в году? Сколько компания сможет сэкономить в год, если снизит стоимость наладки до $25 за производственный цикл?
Решение: здесь C2 = 5, N = 200, C1=100, Q = 20000