Коэффициент Джини
Рассчитать коэффициент Джини можно воспользовавшись сервисом Кривая Лоренца.Рассчитаем коэффициент Джини на основе данных о распределении общего объема денежных доходов населения России в 2006 г. по квинтильным группам:
| 20-ти процентные группы населения | Объем денежных доходов населения в % к итогу |
| первая (с наименьшими доходами) | 5,4 |
| вторая | 10,1 |
| третья | 15,1 |
| четвертая | 22,6 |
| пятая (с наивысшими доходами) | 46,8 |
| ВСЕГО | 100 |
Для исчисления коэффициента Джини необходимо рассчитать величины pi и qi.
В каждой из выделенных групп находится по 20% населения, что в долях единицы составляет 0,2 , соответственно получаем:
p1 = 0.2; p2 = 0.2+0.2 = 0.4; p3 = 0.2+0.2+0.2 = 0.6; p4 = 0.2+0.2+0.2+0.2 = 0.8; p5 = 0.2+0.2+0.2+0.2+0.2 = 1.0
Аналогичным образом рассчитывается величина qi , но при этом используются данные о доле каждой группы в общем объеме денежных доходов населения:
q1 = 0.054; q2 = 0.054+0.101 = 0.155; q3 = 0.054+0.101+0.151 = 0.306;
q4 = 0.054+0.101+.151+0.226 = 0.532; q5 = 0.054+0.101+0.151+0.226+0.468 = 1.0
Полученные результаты представим в виде таблицы, в которой проведем расчет величин piqi+1 и pi+1qi.
| pi | qi | piqi+1 | pi+1q |
| 0,2 | 0,054 | 0,0310 | – |
| 0,4 | 0,155 | 0,1224 | 0,0216 |
| 0,6 | 0,306 | 0,3192 | 0,0930 |
| 0,8 | 0,532 | 0,8000 | 0,2448 |
| 1,0 | 1,0 | – | 0,5320 |
| ВСЕГО | 1,2726 | 0,8914 |
KL = Σpiqi+1 - Σpi+1qi = 1,2726 – 0,8914 = 0,3812
Коэффициент Джини изменяется в пределах от 0 до 1. Причем, чем больше его значение отклоняется от нуля и приближается к единице, тем в большей степени доходы сконцентрированы в руках отдельных групп населения.
Пример №1. По данным исследования, в распределении доходов страны кривая Лоренца имеет вид y=x3/2, где x – доля населения, y – доля доходов населения. Найдите коэффициент Джини.
Решение.
Воспользуемся определением коэффициент Джини.
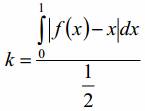
С помощью программы нарисуем графики:
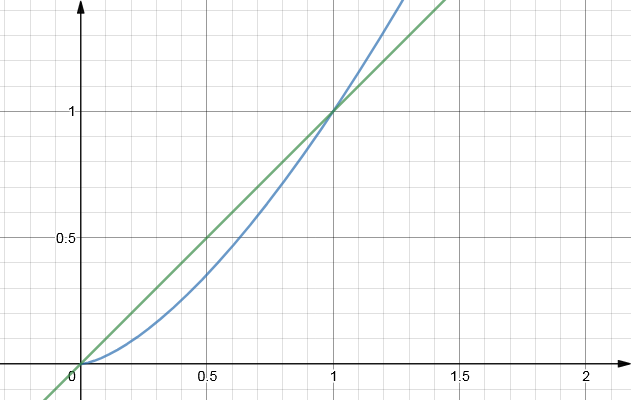
Заштрихованная область - искамая площадь -как разница площадей между функциями y=x и y=x3/2.
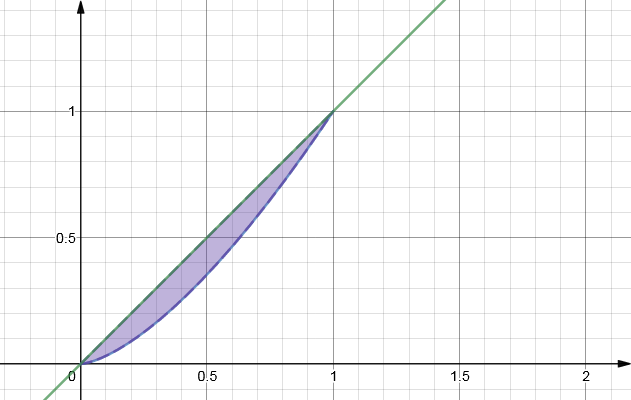
Получим (см. как найти интеграл)
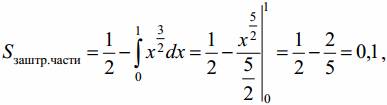
Тогда
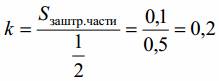
Таким образом, так как коэффициент Джини достаточно мал, то распределение доходов среди населения в данной стране достаточно равномерное.