Задача межотраслевого баланса
Три отрасли промышленности I, II и III являются производителями и в то же время потребителями некоторой продукции. Их взаимосвязь определяет матрица А коэффициентов прямых затрат
,
в которой число aij, стоящее на пересечении i -ой строки и j -го столбца равно xij/Xj, где xij– поток средств производства из i-ой отрасли в j-ую, а Xj – валовой объем продукции j-ой отрасли (все объемы продукции выражаются в единицах стоимости).
Задан также вектор
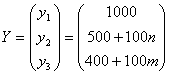объемов конечной продукции.
1. Составить уравнение межотраслевого баланса.
2. Решить систему уравнений межотраслевого баланса, то есть найти объемы валовой продукции каждой отрасли X1, X2, X3 обеспечивающие потребности всех отраслей и изготовление конечной продукции Y. (Расчеты рекомендуется производить с точностью до двух знаков после запятой)
3. Составить таблицу Х потоков средств производства xij.
4. Определить общие доходы каждой отрасли
.
5. Результаты расчетов оформить в виде таблицы межотраслевого баланса:
| потребляющие отрасли отрасли производящие |
I |
II |
III |
конечный продукт |
валовой продукт |
|
I |
x11 |
x12 |
x13 |
y1 |
X1 |
|
II |
x21 |
x22 |
x23 |
y2 |
X2 |
|
III |
x31 |
x32 |
x33 |
y3 |
X3 |
|
общий доход |
P1 |
P2 |
P3 |
|
|
|
валовой продукт |
X1 |
X2 |
X3 |
|
|
Найти матрицу коэффициентов полных затрат по формуле AII=(E-A)-1, где Е – единичная матрица размера 3x3.