Индекс переменного состава
Назначение сервиса. При анализе средних величин в онлайн режиме рассчитываются:- индекс переменного состава, индекс постоянного состава, индекс структурных сдвигов.
- мультипликативная и аддитивная индексные двухфакторные модели среднего показателя (например, среднедушевого товарооборота, среднего товарооборота, средней фондоотдачи или средней рентабельности).
см. пример решения и оформления: индекс структурных сдвигов.
Рассчитайте:
- Индекс затрат рабочего времени на один гарнитур переменного и фиксированного состава.
- Индекс структурных сдвигов.
- Взаимосвязь рассчитанных индексов.
При изучении качественных показателей часто приходится рассматривать изменение средней величины индексируемого показателя для определенной однородной совокупности. Будучи сводной характеристикой качественного показателя, средняя величина складывается как под влиянием значений показателя у отдельных единиц совокупности, так и под влиянием соотношения их весов («структуры совокупности»).
Пример №1. Индекс переменного состава себестоимости продукции равен 1.1. Индекс фиксированного состава себестоимости продукции равен 0,95. Определите индекс структурных сдвигов себестоимости продукции, сделайте выводы.
Решение.
Ic.c = Iп.с./Iф.с. = 1,1/0,95 = 1,158
За счет изменения структуры себестоимости продукции, средняя себестоимости продукции выросла на 15,8%.
Пример №2. Имеются следующие данные о затратах на продукцию и прибыли предприятия за два периода, млн. руб.
| Прибыль от реализации продукции. | Рентабельность затрат | ||
| базисный | отчетный | базисный | отчетный |
| 3 | 3 | 0,2 | 0,2 |
| 2 | 4 | 0,125 | 0,286 |
Решение.
а) индекс рентабельности переменного состава
Рассчитаем средние рентабельности за каждый период:
Средняя рентабельность за отчетный период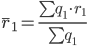
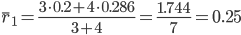
Средняя рентабельность за базисный период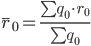
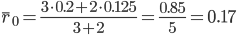
Соответственно, индекс рентабельностей переменного состава (индекс средних величин) будет представлять собой отношение: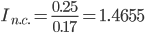
За счет всех факторов рентабельность возросла на 46.55%.
б) индекс рентабельности фиксированного (постоянного) состава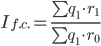
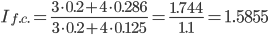
За счет изменения структуры рентабельности средняя рентабельность возросла на 58.55%
в) индекс влияния изменения структуры прибыли на динамику средней рентабельности.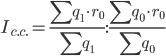
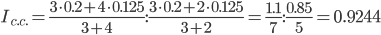
Сравнивая формулы, полученные для расчета вышеуказанных индексов, нетрудно заметить, что индекс структурных сдвигов равен отношению индекса переменного состава и индекса фиксированного состава, т.е.: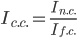
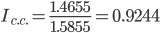
За счет изменения структуры затрат средняя рентабельность снизилась на 7.56%
Рассмотрим разложение по факторам абсолютного изменения качественного показателя в однородной совокупности.
Абсолютный прирост средних рентабельностей по всем группам будет рассчитываться следующим образом: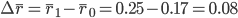
Изменение средней рентабельности по всем группам только за счет изменения средней рентабельности по отдельным группам будет рассчитываться по формуле: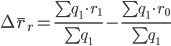
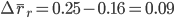
Аналогичные рассуждения проводятся и для расчета изменения средней рентабельности по всем группам только за счет изменения структуры затрат: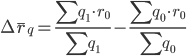
Очевидно, что общий абсолютный прирост средних рентабельностей по всем группам равен сумме факторных изменений: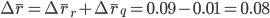
Пример №3. Имеются следующие данные по предприятию:
| Категория персонала | Среднесписочная численность работающих, чел. | Средняя заработная плата за месяц тыс. руб. | ||
| Базисный месяц | Отчетный месяц | Базисный месяц | Отчетный месяц | |
| Руководители | 18 | 16 | 18,0 | 23,0 |
| Специалисты | 203 | 210 | 14,6 | 15,8 |
| Рабочие | 110 | 112 | 9,8 | 10,6 |
Абсолютный прирост фонда зарплаты по предприятию в целом за счет изменения: а) средней зарплаты, б) численности работников. Сделайте выводы.