Индексы средней заработной платы переменного, постоянного состава и структурных сдвигов
Имеются следующие данные о заработной плате работников трех предприятий:| Число работников: базисный период | Число работников: Отчетный период | Заработная плата: отчетный период | Себестоимость единицы продукции: отчетный период |
| 60 | 50 | 11670 | 11700 |
| 40 | 45 | 11750 | 11800 |
| 100 | 120 | 11820 | 11900 |
1) среднюю заработную плату за каждый период;
2) индексы средней заработной платы переменного, постоянного состава и структурных сдвигов.
Решение осуществляем с помощью калькулятора индекс переменного состава
а) индекс заработной платы переменного состава
Рассчитаем средние заработной платы на производительность труда:
Средняя заработной платы за отчетный период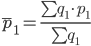
Средняя заработной платы за базисный период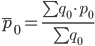
Таким образом, можно сказать, что средняя заработной платы на производительность труда по всем группам равна сумме произведений средней заработной платы по группам (качественный показатель) на долю в физическом объеме соответствующей группы (количественный показатель).
Доля в количественном объеме товара в данном примере определяет структуру объема продукции.
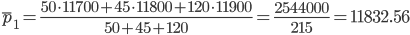
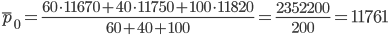
Соответственно, индекс заработной платы переменного состава (индекс средних величин) будет представлять собой отношение:
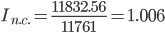
За счет всех факторов заработной платы возросла на 0.61%
По аналогии с построением факторных агрегатных индексов построим факторные индексы.
б) индекс себестоимости фиксированного (постоянного) состава
Чтобы определить влияние только средней заработной платы по разным группам товара на изменение средней заработной платы по всей совокупности в формуле индекса заработной платы переменного состава необходимо устранить влияние изменения структуры физического объема.
Это достигается путем фиксирования значения доли (количественный показатель) на отчетном уровне. Получаемый индекс называется индексом фиксированного (постоянного) состава и рассчитывается по формуле:
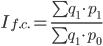
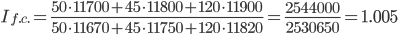
За счет изменения структуры себестоимости средняя себестоимость возросла на 0.53%
в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости
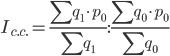
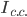 =
= 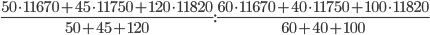 =
= 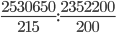 =
= 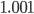
Сравнивая формулы, полученные для расчета вышеуказанных индексов, нетрудно заметить, что индекс структурных сдвигов равен отношению индекса переменного состава и индекса фиксированного состава, т.е.:
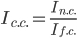
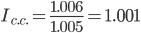
За счет изменения структуры выработанной продукции средняя заработной платы возросла на 0.0805%
Кроме этих трех индексов для однородной совокупности может быть рассчитан общий индекс физического объема:
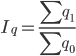
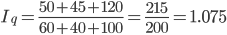
Общий индекс стоимости равен:
IQ = Iп.c. x Iq = 1.006 x 1.075 = 1.081
Рассмотрим разложение по факторам абсолютного изменения качественного показателя в однородной совокупности.
Абсолютный прирост средних заработной платы на производительность труда по всем группам будет рассчитываться следующим образом:
Δp=p1-p0 = 11832.56 - 11761 = 71.56
Изменение средней заработной платы на производительность труда по всем группам только за счет изменения средней заработной платы по отдельным группам будет рассчитываться по формуле:
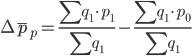
Δpp = 11832.56 - 11770.47 = 62.09
Аналогичные рассуждения проводятся и для расчета изменения средней заработной платы по всем группам только за счет изменения структуры физического объема:
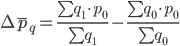
Δpq = 11770.47 - 11761 = 9.47
Очевидно, что общий абсолютный прирост средних заработной платы по всем группам равен сумме факторных изменений:
Δp = Δpp + Δpq
Пример. Имеются данные по одному из предприятий:
| Вид продукции | Ед. измерения | Себестоимость, руб. | Выпущено продукции в отчетном периоде, тыс. ед. | |
| Базисный период | Отчетный период | |||
| 1 | м | 30 | 34 | 4,8 |
| 2 | т | 1500 | 1620 | 0,3 |
| 3 | шт | 42 | 51 | 6,4 |
1) индивидуальные индексы себестоимости продукции
2) общий индекс себестоимости продукции
3) определите, на сколько возросли затраты на производство продукции за счет среднего увеличения себестоимости
Решение:
1) индивидуальные индексы себестоимости продукции
| Базисный период | Отчетный период | индекс себестоимости продукции (отчет / базис) |
| 30 | 34 | 1,13 |
| 1500 | 1620 | 1,08 |
| 42 | 51 | 1,21 |
2) общий индекс себестоимости продукции
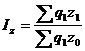
3) определите, на сколько возросли затраты на производство продукции за счет среднего увеличения себестоимости
∆Zz = ∑q1 • z1 - ∑q1 • z0 = 975.6 - 862.8 = 112.8 тыс. руб.
За счет изменения себестоимости общие затраты возросли на 13.07% или на 112.8 тыс. руб.