Индекс средней цены
Задача 44. Продажа товара А на рынках города за два периода:| Рынок | Базисный период | Отчетный период | ||
| цена за 1кг, руб. | продано, кг | цена за 1 кг, руб. | продано, кг | |
| 1-й 2-й 3-й | 18,0 16,0 19,0 | 180 230 165 | 19 18 22 | 170 250 184 |
- индекс средней цены (индекс цен переменного состава);
- индекс цен в неизменной структуре продажи (индекс цен постоянного состава);
- индекс структурных сдвигов в объеме продажи.
а) индекс средней цены (индекс цен переменного состава)
Рассчитаем средние цены на товар А:
Средняя цена за отчетный период
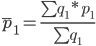
Средняя цена за базисный период
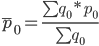
Из этих формул следует, что средняя цена по всем группам зависит от средней цены на товар А по отдельным группам и доли физического объема продаж в каждой из этих групп.
Таким образом, можно сказать, что средняя цена на товар А по всем группам равна сумме произведений средней цены по группам (качественный показатель) на долю в физическом объеме соответствующей группы (количественный показатель).
Доля в количественном объеме товара в данном примере определяет структуру объема продукции.
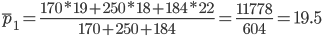
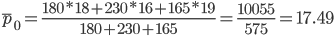
Соответственно, индекс цен переменного состава (индекс средних величин) будет представлять собой отношение:
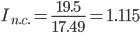
За счет всех факторов цена возросла на 11.51%
По аналогии с построением факторных агрегатных индексов построим факторные индексы.
Чтобы определить влияние только средней цены по разным группам товара на изменение средней цены по всей совокупности в формуле индекса цен переменного состава необходимо устранить влияние изменения структуры физического объема.
Это достигается путем фиксирования значения доли (количественный показатель) на отчетном уровне. Получаемый индекс называется индексом фиксированного (постоянного) состава и рассчитывается по формуле:
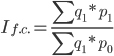
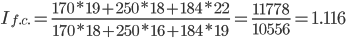
За счет изменения структуры цены средняя цена возросла на 11.58%
в) индекс влияния изменения структуры производства продукции на динамику средней цены
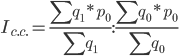
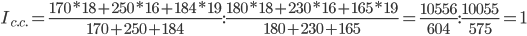
Сравнивая формулы, полученные для расчета вышеуказанных индексов, нетрудно заметить, что индекс структурных сдвигов равен отношению индекса переменного состава и индекса фиксированного состава, т.е.:
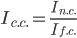
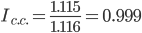
За счет изменения структуры выработанной продукции средняя цена снизилась на 0.058%
Кроме этих трех индексов для однородной совокупности может быть рассчитан общий индекс физического объема:
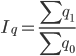
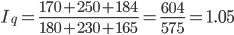
Общий индекс стоимости равен:
IQ = Iп.c. x Iq = 1.115 x 1.05 = 1.171
Рассмотрим разложение по факторам абсолютного изменения качественного показателя в однородной совокупности.
Абсолютный прирост средних цен на товар А по всем группам будет рассчитываться следующим образом:
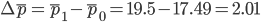
Изменение средней цены на товар А по всем группам только за счет изменения средней цены по отдельным группам будет рассчитываться по формуле:
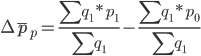
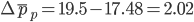
Аналогичные рассуждения проводятся и для расчета изменения средней цены по всем группам только за счет изменения структуры физического объема:
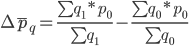
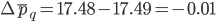
Очевидно, что общий абсолютный прирост средних цен по всем группам равен сумме факторных изменений:
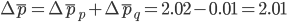
Задача 45. Выпуск одноименной продукции и ее себестоимость по двум предприятиям за два периода:
| Предприятие | Базисный период | Отчетный период | ||
| себестоимость единицы продукции, тыс. руб. | произведено, тыс. шт. | себестоимость единицы продукции, тыс. руб. | произведено, тыс. шт. | |
| 1е 2-е | 8 10 | 50 46 | 10 11 | 45 40 |
- индекс средней себестоимости (индекс переменного состава);
- индекс себестоимости в неизменной структуре производства (индекс постоянного состава);
- индекс структурных сдвигов в производстве продукции.
Решение.
а) индекс себестоимости переменного состава
Рассчитаем средние себестоимости на Выпуск продукции:
Средняя себестоимость за отчетный период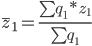
Средняя себестоимость за базисный период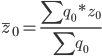
Из этих формул следует, что средняя себестоимость по всем группам зависит от средней себестоимости на Выпуск продукции по отдельным группам и доли физического объема выработки продукции в каждой из этих групп.
Таким образом, можно сказать, что средняя себестоимость на Выпуск продукции по всем группам равна сумме произведений средней себестоимости по группам (качественный показатель) на долю в физическом объеме соответствующей группы (количественный показатель).
Доля в количественном объеме товара в данном примере определяет структуру объема продукции.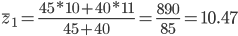
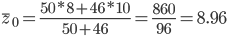
Соответственно, индекс себестоимости переменного состава (индекс средних величин) будет представлять собой отношение: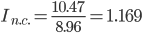
За счет всех факторов себестоимость возросла на 16.88%
По аналогии с построением факторных агрегатных индексов построим факторные индексы.
б) индекс себестоимости фиксированного (постоянного) состава
Чтобы определить влияние только средней себестоимости по разным группам товара на изменение средней себестоимости по всей совокупности в формуле индекса себестоимости переменного состава необходимо устранить влияние изменения структуры физического объема.
Это достигается путем фиксирования значения доли (количественный показатель) на отчетном уровне. Получаемый индекс называется индексом фиксированного (постоянного) состава и рассчитывается по формуле: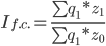
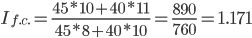
За счет изменения структуры себестоимости средняя себестоимость возросла на 17.11%
в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости
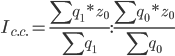
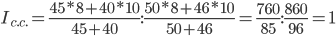
Сравнивая формулы, полученные для расчета вышеуказанных индексов, нетрудно заметить, что индекс структурных сдвигов равен отношению индекса переменного состава и индекса фиксированного состава, т.е.: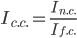
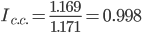
За счет изменения структуры выработанной продукции средняя себестоимость снизилась на 0.19%
Кроме этих трех индексов для однородной совокупности может быть рассчитан общий индекс физического объема:
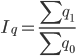
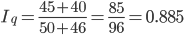
Общий индекс стоимости равен:
IQ = Iп.c. x Iq = 1.169 x 0.885 = 1.035